Голографическая модель Вселенной.
Книга 3. Происхождение материи
8. Образование молекул (внешнее пространство)
Покажем на примере нескольких молекул, какую роль играет в их образовании голограммы матриц 1,2,3 порядка. Голограмма, несущая в себе образ интегральной структуры мироздания, участвует при интеграции не только атомов, но и молекул, которые также образуются на их основе. Поэтому молекулы формируются в результате преобразования нелокализованных потоков энергий в матрице во внешние связи атомов, которые объединяют их в молекулы.
Каждая матрица – это условное изображение расходящихся волн, которые формируют пространство корпускул (здесь под корпускулами будем понимать атомы и молекулы.). Схема электронных оболочек в атоме соответствует голограмме, фактически повторяя интегральную структуру мироздания. В матрице второго порядка имеется всего 20 свободных квартов, это соответствуют 20-ти атомным орбиталям, что в два раза больше, чем максимальное количество электронов, которые могут быть у атома второго периода неона (Ne - 10 электронов). Это объясняется тем, что рисунок матрицы отражает не одну расходящуюся волну, а две. Так как по Козыреву, ход времени вызывает пару противоположно направленных сил или пару моментов вращения. Матрица третьего порядка обладает 36 «вакансиями», которые заполняют электроны.
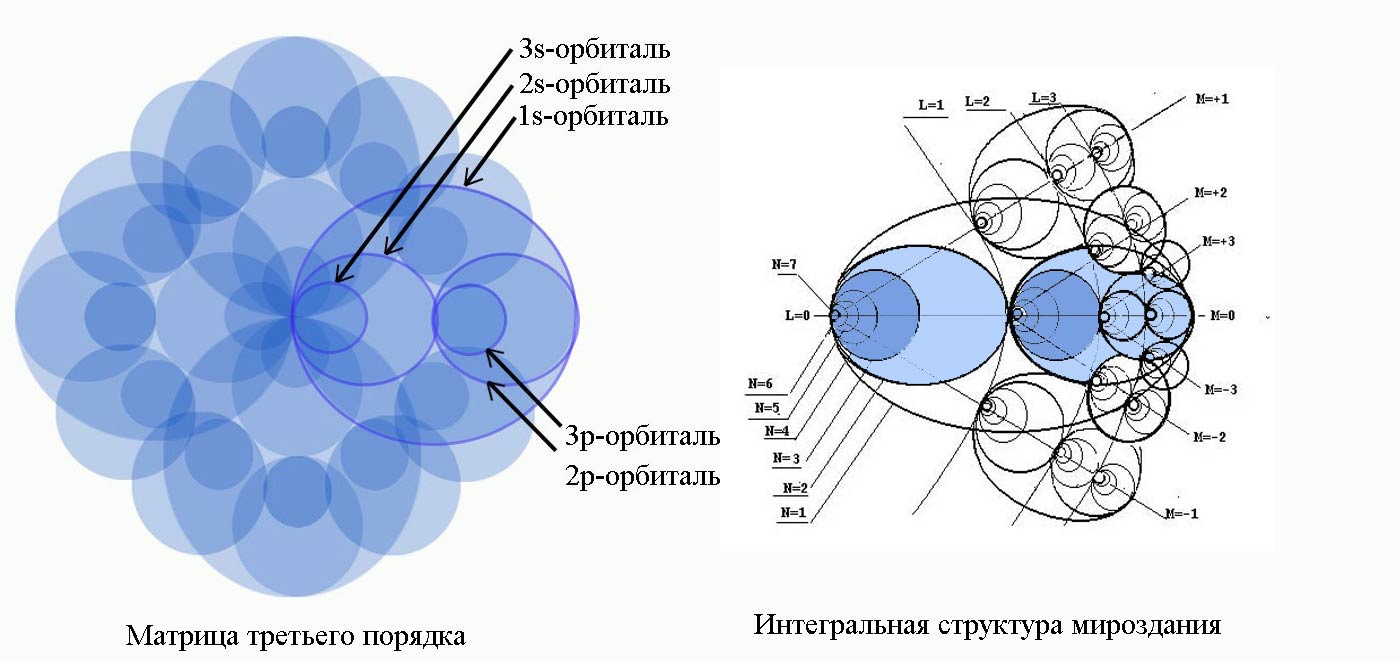
Рис.8-1. Матрица третьего порядка повторяет интегральную структуру мироздания
Матрицу можно также рассматривать в соответствии с современным представлением строения электронной оболочки в атоме (Рис.8-1). Каждой атомной орбитали, которая отвечает за состояние отдельного электрона в атоме, соответствует свой кварт. S-орбитали находятся в центральных квартах, принадлежат центральной точке L=0. Диаметр кварта уменьшается с ростом числа n. Поэтому диаметр 3s-орбитали меньше, чем диаметр 2s-орбитали. Энергия электрона также связана с числом n. Поэтому энергия связи электрона с атомом 1s-орбитали самая большая. Р-орбитали находятся за границей 2s-орбиталей, принадлежат особой точке L=1. Элемент матрицы, который выбран для обозначения орбиталей соответствует закрашенному элементу интегральной структуры мироздания (ИСМ). На схеме ИСМ видно, как дальше строятся матрицы более высоких порядков. Например, d-орбитали находятся за границей 2р-орбиталей, принадлежат особым точкам L=3.
8.1. Молекула воды
Посмотрим, например, матрица второго порядка, которая является «окном» в проявленный мир, продуцирует атомы кислорода. Каждый атом, продуцируемый матрицей, несет в себе полный образ ее голограммы, хотя только часть квартов заполнена упорядоченной энергией. На рис.8-1 схематично показан атом кислорода в виде точки и структура его внешнего пространства.
Покажем, что в образовании корпускул их внешняя структура в виде голограммы не менее важна, чем внутренняя. В целом схема (рис.8-1), которая представляет собой голограмму, отображает внешнее пространство строения атомов (в данном случае водорода и кислорода) или молекул (в нашем случае – воды). Сами атомы изображены в центре матрицы в виде точек, которые в пространстве разнесены, т.к. не могут занимать один и тот же объем. Зато внешнее их пространство совмещено, т.к. u, d -бозоны могут накапливаться на одном уровне. Причем на схеме хорошо видно, что они объединяясь попарно, образуют частицу-волну с целым спином, что позволяет им накапливаться на одном уровне, образуя границы внешнего пространства.
По сравнению с матрицей второго порядка (рис.8-1), видно, что энергия в атоме кислорода локализована только в некоторой части квартов, которая изображена в виде сфер. Каждая из сфер соответствует одному из электронов атома. (Продолжаем пользоваться старой терминологией в силу устоявшихся привычек, хотя понимаем, что электронов в атоме нет). Т.к. в атоме кислорода содержится 8 электронов, то и голограмма содержит 8 сфер. Но большая часть энергии не локализована, поэтому на голограмме атома кислорода она никак не отображена. Если сравнивать голограммы просто атомов и молекулы с матрицей второго порядка, то видно, что локализованных потоков (сфер) в молекуле больше. Это означает, что в голограмме молекулы воды, которая состоит из двух атомов водорода и одного атома кислорода, энергия находится в более упорядоченном состоянии, чем в каждом из атомов отдельно. Следовательно, энергетически она находится в более выгодном положении.
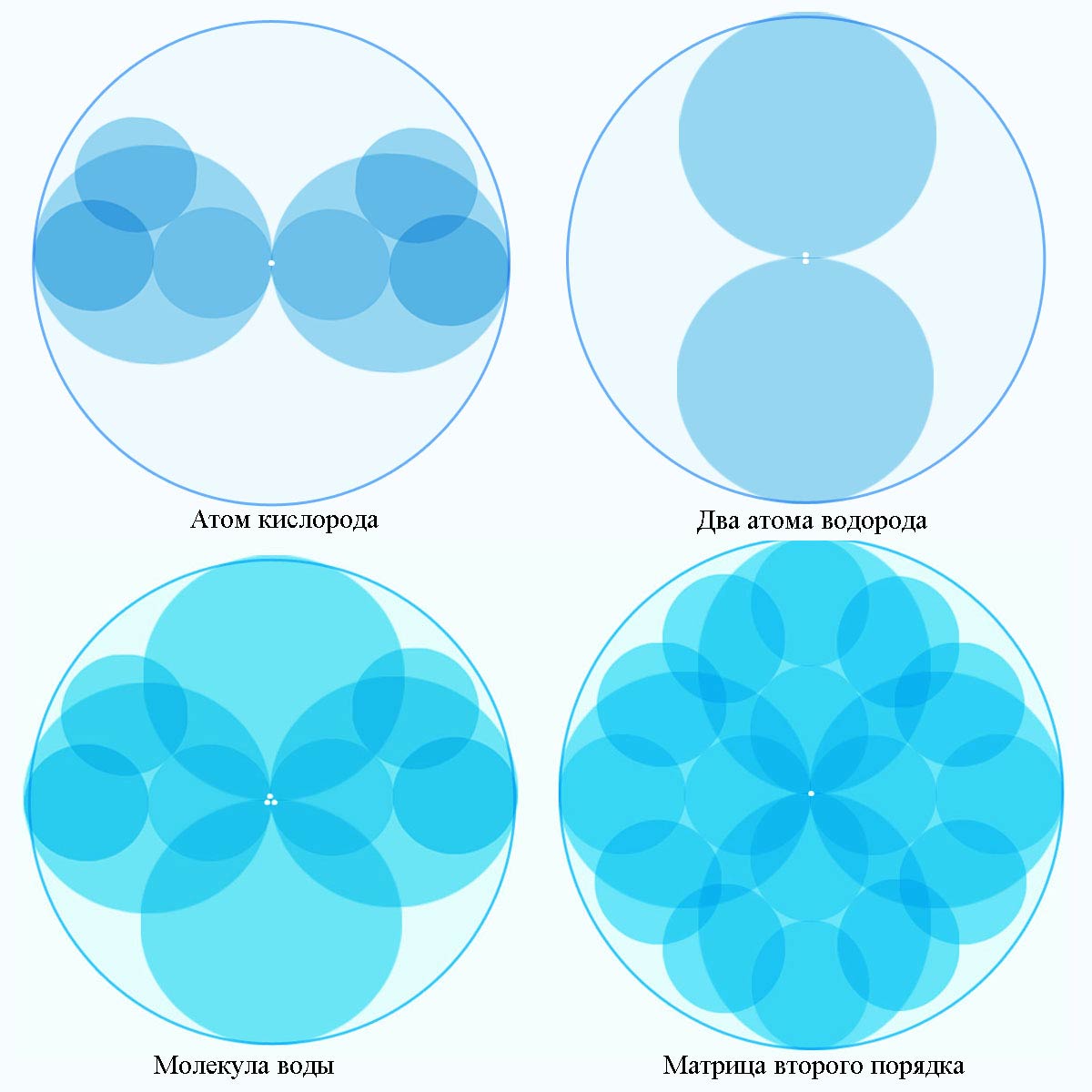
Рис.8-2.Голограммы атомов водорода, кислорода и молекулы воды (структура внешнего пространства атомов и молекул)
Поэтому, когда матрицы второго порядка генерируют материю в виде всей молекулы целиком, то это является более выгодным процессом с точки зрения потенциальной энергии. Очевидно, что благодаря такой голографической матрице, вначале появляется модель будущей молекулы, а потом по ее образу и подобию штампуются сами молекулы. Образованные матрицей молекулы обладают более низким значением потенциальной энергии, чем составляющие ее атомы, т.к. часть энергии преобразовалась во внутренние связи молекулы.
Теперь посмотрим, насколько реально такое событие в природе. А оно действительно происходит, и тому есть доказательства в виде спектральных линий воды, обнаруженных в спектре излучения Солнца. Причем в виде молекул! Это означает, что на Солнце, вещество которого может находиться исключительно в виде плазмы, существуют трехатомные молекулы воды.
Ответ на вопрос, каким образом вода могла появиться на Солнце, теперь не представляется сложным, т.к. это и есть результат действия матрицы второго рода. Поскольку существующие во внутреннем пространстве Солнца особые точки способны генерировать молекулы целиком, что является энергетически более выгодным процессом, то вещество на Солнце также генерируется в виде молекул. Конечно, в условиях высоких температур и давления такие молекулы существовать долго не могут, поэтому распадаются на составляющие их компоненты.
Заметим, что ранее воду находили также и в спектрах других звезд, и пытались их объяснить побочными причинами. Например, тем, что по диску звезды движется вращающаяся вокруг нее планета, в воздушной атмосфере которой находятся пары воды.
Обнаруженная на Солнце вода свидетельствует о том, что современная наука описывает физику процессов образования молекул далеко не полностью. Помимо химических превращений молекул, существуют и другие способы их появления. Таким способом является возникновение молекулы в особых точках внутренних хронооболочек космических тел, будь то планета или звезда.
8.2. Кристаллический углерод
Рассмотрим еще один пример того, как матрица второго порядка продуцирует вещество в виде кристаллического углерода. В отличие от предыдущего примера, когда матрица второго порядка продуцировала молекулу воды, в этом случае происходит образование не молекулы, а кристалла. Покажем, что образование сразу одного элемента кристалла является более выгодным энергетическим процессом, чем образование того же количества свободных атомов.
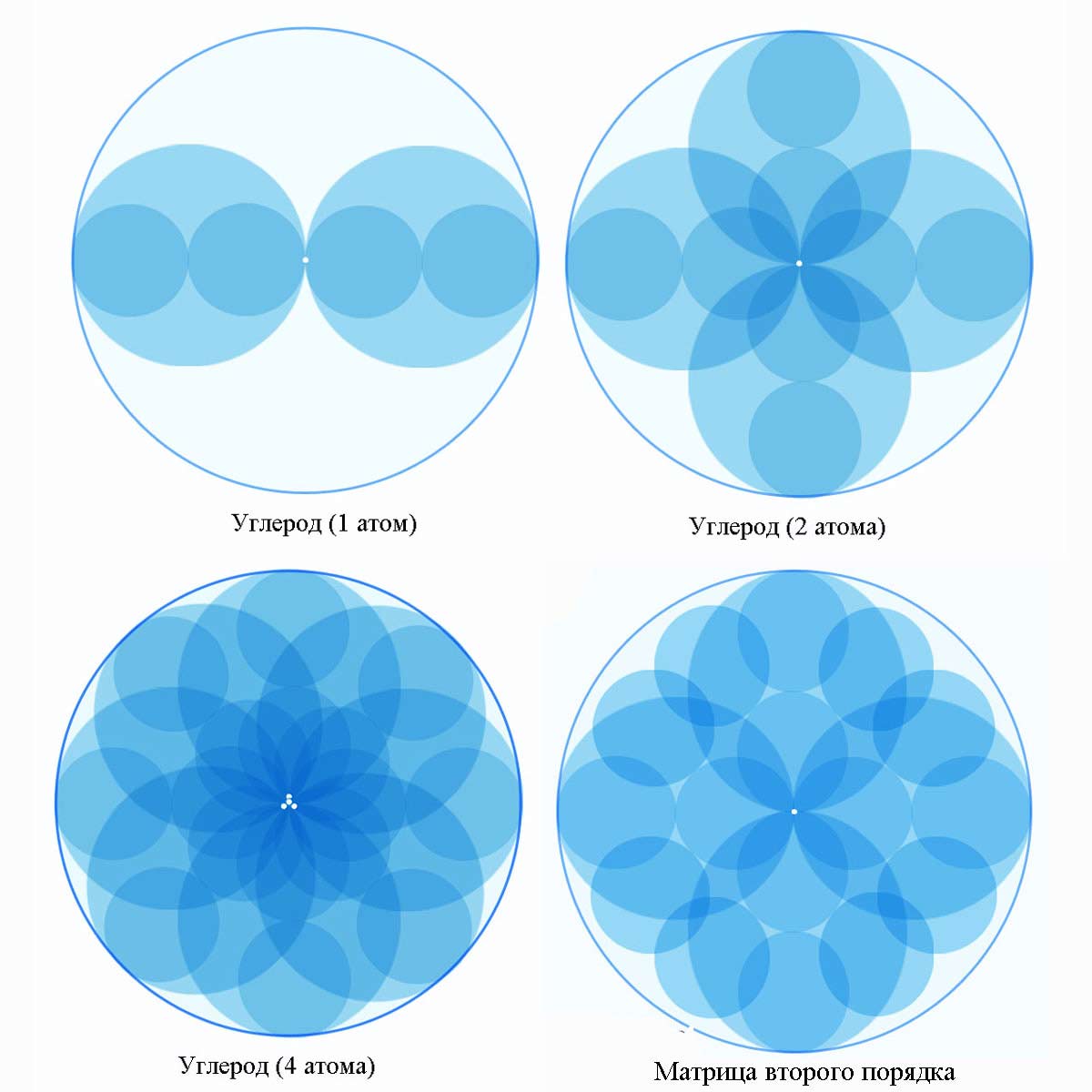
Рис.8-3. Голограмма кристаллического углерода
Вначале в центре матрицы продуцируется первый атом углерода, несущий в себе голограмму всей матрицы. Атом углерода имеет 6 электронов, поэтому голограмма имеет шесть заполненных энергией квартов, изображенных в виде сфер. После того, как заполнятся все энергетические уровни первого атома углерода, в той же матрице начинают заполняться свободные кварты в виде второго атома углерода (рис.8-3б). Поскольку остаются свободные места в матрице, то и они продолжают заполняться энергией. Когда внутри заполнятся все свободные кварты, что соответствует четырем атомам углерода, готовая структура оказывается в проявленном мире (рис.8-3в). Поскольку у этой структуры все энергетические потоки находятся в связанном состоянии, то энергетически она более выгодна, чем структура, состоящая из четырех отдельных атомов.
Если сравнить голограмму кристаллического элемента четырех атомов углерода с матрицей второго порядка (рис.8-3д), то видно, что энергия четырех s- орбиталей у двух атомов заполнила р-орбитали, также видно, что 4 орбитали «лишние» т.к. 4 атома углерода имеют 24 электрона, а у матрицы только 20 «вакансий». Поэтому четыре орбитали оказываются сдвоенными, т.к. бозоны могут накапливаться на одном уровне, именно они в дальнейшем становятся стимулом к захвату всех аналогичных структур и определяют образование ковалентных связей между атомами.
Как видно по матрице все четыре атома углерода «стараются» занять энергетически наиболее выгодные места, поэтому они располагаются в углах тетраэдра. Таким образом, матрица продуцирует не по одному атому, а сразу четверку атомов в виде одного структурного элемента кристалла. После этого матрица второго порядка снова продуцирует одновременно еще связанных между собой 4 атома углерода, которые, благодаря четырем «валентным» связям, стремятся объединиться с первой четверкой атомов, в результате чего рождается кристалл. Так внешняя структура, выполненная в виде голограммы, формирует образование и рост кристалла.
8.3. Внутренне пространство молекул и атомов
До сих пор мы рассматривали голограммы атомов и молекул как внешние пространства корпускул. При этом сами корпускулы в какой-то мере повторяют в себе те же самые принципы квантования хронооболочек, хотя имеются и различия. Посмотрим, в чем эти отличия проявляются.
Корпускулы, которые мы представляем в виде атомов и молекул обладают внешним и внутренним пространством. Внешнее пространство мы рассмотрели, обратимся теперь к внутреннему пространству корпускул. Вначале посмотрим внутреннее пространство атомов. Для того, чтобы это сделать, вспомним, что атом состоит из ядра и электронных оболочек. Поэтому нам придется рассматривать новую систему с позиции ядра атома. В этом случае мы также можем выделить два пространства - внутреннее и внешнее. Внешнее пространство определяется электронами, которые располагаются в виде электронных облаков, внутреннее пространство определяется протонно-нейтронным составом. Причем количество протонов в атоме является основным фактором, который определяет его расположение в системе Менделеева, его порядковый номер и его химические свойства. Поэтому в первую очередь нас будет интересовать количественный состав протонов в атоме и их взаимное расположение в ядре.
Как мы знаем, ряд химических элементов в таблице Менделеева открывается атомом водорода, который в своем ядре имеет всего один протон. Каждый последующий атом содержит в своем ядре на один протон больше. Расположение протонов в ядре, будем считать, должно обладать минимальным уровнем потенциальной энергии, что соответствует симметричным формам, которые в свою очередь обладают минимальным уровнем энтропии. Поэтому вначале рассмотрим, какие варианты симметрии могут существовать для расположения сфер одного диаметра в пространстве.
Одна, две, три сферы, создающие плотную упаковку в пространстве, для нас не представляют особого интереса, т.к. здесь нет особых вариантов, поскольку существует только один способ их расположения. Для большего количества сфер нам придется рассмотреть несколько вариантов их расположения в пространстве. Сразу выделим два принципиально различных способа расположения – вертикальный и горизонтальный. Отличаются они друг от друга тем, что при горизонтальном расположении сферы находятся в одной плоскости, а при вертикальном – в разных плоскостях. Когда происходит дробление хронооболочек внешнего пространства, то обычно образуется плоский вариант (горизонтальное расположение сфер), для внутреннего пространства – объемный вариант (вертикальное расположение сфер). На рисунке показаны оба варианта расположения для 5 и 6 сфер.

Рис.8-4. Расположение пяти сфер в пространстве

Рис.8-5. Расположение шести сфер в пространстве
Однако наибольший интерес для нас будет представлять такое расположение сфер в пространстве, которое отвечает образованию правильных многогранников. Причем будем считать, что сферы располагаются не в углах многогранников, а представляют собой грани. Тогда 6 сфер образуют гексаэдр, а 8 сфер – октаэдр. Причем образование восьми сфер приводит к тому, что они могут располагаться и в виде куба, и в виде двух взаимно пересекающихся тетраэдров (рис.8-6). В этом случае горизонтальный и вертикальный тип (другими словами, объемные и плоские варианты) дробления совмещены.

Рис.8-6. Образование восьми сфер приводит к тому, что они могут располагаться и в виде куба, и в виде двух взаимно пересекающихся тетраэдров
В случае образование додекаэдра мы имеет просто равномерное распределение 12 одинаковых сфер в пространстве.

Рис. 8-7. Икосаэдр с 12-тью сферами.
Надо отметить, что появление еще одной 13-той сферы внутри додекаэдра оказывается более энергетически выгодно, т.к. при той же поверхности структура включат в себя большее количество элементов. Как известно додекаэдр легко перестраивается в икосаэдр (рис.8-8). На рис.8-7 показан икосаэдр с 12-ю сферами.

Рис.8-8. Додекаэдр и икосаэдр легко перестаиваются друг в друга, тогда центр каждой грани одного многогранника становится вершиной другого многогранника
Взаимное перестроение общего интерференционного поля понять не сложно, т.к. мы знаем, что в куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра - внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба (рис.8-9).

Рис.8-9. В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра - внутри куба
Объемное квантование хронооболочек приводит к тому, что в каждой из них образуются еще несколько, которые также будут квантоваться согласно описанным выше схемам. Например, в каждой хронооболочке тетраэдра может образоваться еще по одному тетраэдру, октаэдру, додекаэдру и т.д. (рис.8-10).

Рис.8-10. Дробление хронооболочек. В каждой из них может образоваться еще по одному тетраэдру, октаэдру, додекаэдру и т.д.
Теперь вполне можно представить, каким может быть расположение хронооболочек в пространстве, образующих голограммы атомов. Образование самих голограмм можно строить исходя из того, что формируемое пространство будет состоять из нескольких оболочек по числу протонов в атоме, т.е. соответствующих его атомному номеру (n). Строя структуру образующегося пространства, надо учесть, что оболочки вначале не могут пересекаться между собой, и должны располагаться так, чтобы представлять собой плотную упаковку, что соответствует минимальному уровню энергии. Впоследствии структуры растущих пространств могут пересекаться между собой.
На рис.8-11 показаны варианты расположения оболочек плотной упаковки для разных атомов. Для каждого числа n плотную упаковку можно представить как в виде сферической (объемной) упаковки, так и в тороидальном (плоском) виде.

Рис. 8-11. Голограммы упаковок для разных типов
Для более сложных случаев мы можем воспользоваться взаиморасположением плотной упаковки атомов в кристаллических решетках. В 1848. французский учёный О.Браве определил 14 видов пространственных решёток кристаллов. В основном решётки Браве делятся на 4 типа (см. рис. 8-12): 1) примитивный – узлы расположены только в вершинах параллелепипеда, 2) базоцентрированный – имеется ещё по одному узлу в центрах двух противолежащих граней, 3) объёмноцентрированный – к примитивному типу добавлен узел в центре ячейки, 4) гранецентрированный – имеется по одному узлу в центре каждой грани.
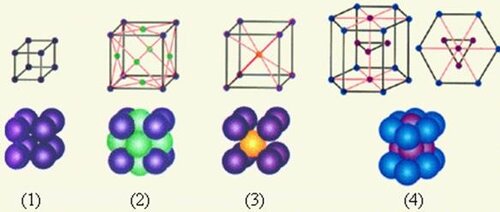
Рис.8-12. Типы кристаллических решеток
Для нас наиболее ценным в этой информации является то, что мы можем представить энергетически наименее емкие варианты расположения хронооболочек. Как видно из рис.8-12 наиболее плотной упаковкой могут обладать 8,9,14,17 хронооболочек, т.е. такое их расположение является энергетически наиболее выгодным. Они обладают наибольшей симметрией и, следовательно, наименьшим уровнем энтропии.
На основании этих представлений мы можем предположить, какие из атомов являются наиболее выгодными с точки зрения энтропии. В первую очередь, это атомы, которые создают правильные многогранники: 4 сферы (тетраэдр) бериллий, 6 сфер (куб или гексаэдр) углерод, 8 сфер (октаэдр) кислород, 9сфер (куб + 1 центральная сфера) фтор, 12 сфер (додекаэдр) магний, 13 сфер (додекаэдр +1 центральная сфера) алюминий, 14 сфер (октаэдр, вписанный в куб) кремний, 17 сфер – хлор, 26 сфер (куб, вписанный в октаэдр, вписанный в додекаэдр) железо. Из перечисленных химических элементов следует исключить бериллий, фтор, магний, хлор вследствие их высокой электроотрицательности или относительно большого орбитального радиуса (рис.8-13).

Рис.8-13. Зависимость орбитальных радиусов атомов от порядкового номера элемента

Рис. 8-14. Значения электроотрицательности в зависимости от порядкового номера элемента
Таким образом, низко энергетическими и низкоэнтропийными остаются кислород, алюминий, кремний, железо. Как известно, в составе земной коры именно эти элементы имеет наибольшее распространение.
8.4. Кристаллическая структура. Кристаллический бор
Образование внутреннего пространства в ядре атома с определенным количеством протонов (атомный номер) соответствует тому, как располагаются оболочки или потенциальные поверхности внешних пространств. Причем происходит как бы «материализация» поверхности. Так самая первая поверхность ограничивала протон. Затем новая поверхность, реализовавшись в результате тройного квантования трех хронооболочек, образовала поверхность, разделяющую ядро атома от внешнего пространства, представленного электронным облаком. Новая структура представляет собой атом водорода.
Следующая реализовавшаяся поверхность разделяет внутреннее пространство атома от внешнего пространства. Таким внешним пространством может быть, например, фрагмент кристалла или молекула. Поэтому мы можем представить общий вид голограммы корпускул на основании порядкового номера атома. Более того, мы можем также утверждать, что внутреннее расположение протонов в атоме определяет и формы образования кристаллических решеток, которые этими атомами могут быть созданы.
В качестве примера посмотрим, как реализуется в пространстве структура кристаллического бора Как известно, существуют несколько его кристаллических модификаций. Для двух из них рентгеноструктурный анализ показал, что кристаллическая структура весьма сложна. Атомы бора образуют в обеих структурах трехмерный каркас подобно атомам углерода в алмазе. Этим объясняется высокая твердость бора. Однако строение каркаса в структурах бора гораздо сложнее, чем в алмазе. Основной структурной единицей в кристаллах бора служат двадцатигранники (икосаэдры), в вершинах каждого из которых находятся 12 атомов (рис.8-15). Икосаэдры соединяются между собой как непосредственно, так и посредством промежуточных атомов Бора, не входящих в состав какого-либо икосаэдра.

Рис. 8.15. Строение кристаллического бора

Рис. 8.16. Варианты расположения пяти хронооболочек в пространстве
Голограмма атома бора (атомный номер - 5), судя по картинке плотной упаковки оболочек, может иметь три разновидности (рис. 8-16). Поэтому в зависимости от того, в каком пространственном модуле рождается атом, он может принимать одну из трех форм, либо объемную, либо плоскую. В нашем случае видно, что структура А имеет пятиугольную форму, а 12 правильных пятиугольников образуют додекаэдр. Поэтому форма А образует данную кристаллическую модификацию.
О бразование кристаллических структур строится на базе голограмм атомов, и зависит от того, в каком пространстве они возникают. На рис.8-17 видно, что в данной кристаллической модификации пространство образовало вначале тетрагональную структуру – квадруполь с одним центральным атомом, затем каждое из подпространств разбилось на 12 оболочек.

Рис. 8-17. Последовательное дробление хронооболочек с образованием в каждой из них фрактальной структуры
Хочу еще раз повторить эту основную идею. Кристаллический бор данной модификации будет образовываться только тогда, когда внешняя структура пространства обладает такой же конфигурацией. А подобная структура пространства вполне могла бы образоваться при квантовании хронооболочек планеты.
8.5. Молекула метана
Энергетически выгоднее генерировать не отдельные атомы, а целиком молекулы. Поэтому углерод будет рождаться не отдельными молекулами, а сразу в составе молекул метана. Голограмма атома углерода, имеющего шесть протонов, представляет собой гексаэдр. Четыре атома водорода составляют тетраэдр, всего на молекулу метана приходится 10 протонов. В общем виде десять протонов можно представить, как тетраэдр вписанный в гексаэдр. Интересно, что примерно такую же структуру имеет молекула воды Н2О, которая имеет восемь протонов, взятых от кислорода, и два протона от двух атомов водорода. Но то, каким составом будет обладать данная голограмма, зависит от структуры окружающего пространства.
Поэтому только окружающая форма пространства задаст генерацию либо молекулы метана, либо молекулы воды, либо атома неона, также имеющего 10 протонов.

Рис.8-18. Хронооболочки, образующие структуру метана. А - голограмма метана.
Таким образом, особые точки в пространстве становятся родоначальниками не только атомов, но и различного типа молекул. Причем атомный состав молекулы зависит о того, хронооболочки каких модулей принимают участие в общей интерференционной картине. Из этого можно сделать еще один очень интересный вывод. Возьмем, например, вариант тетраэдра. Четыре его протона способны реорганизоваться в любом из следующих вариантов: 4 молекулы водорода, 2 молекулы гелия, 1 атом гелия и 2 молекулы водорода, 1 атом лития и 1 атом водорода, 1 атом бериллия. Как видно, тетраэдр может формировать семь разных событий. В какой взаимозависимости могут реализоваться эти события, будет зависеть от внешних и внутренних условий, хотя понятно, что эти события не равновероятны. Следовательно, в тетраэдре могут генерироваться в качестве сходящейся волны 7 разных событий, которые можно представить в виде корпускул, т.е. легких атомов или молекул. Они же (корпускулы) являются основной формой записи происходящих событий.
Поэтому надо ясно понимать, что квантование хронооболочек с их последующим преобразованием не происходит случайно, это закономерное событие, подготовленное в ходе предыдущих процессов. Все события последовательно записываются в виде корпускул, расположенных в строгом порядке. Поэтому на корпускулярном уровне мы получаем нечто вроде записи информации о событии, составленном в виде предложения из слов (корпускул). Следовательно, любая молекула или молекулярная цепочка – это своего рода ключ к пространству, т.к. на его основе воссоздается первоначальный образ пространства. Это одно из главных свойств физической материи.
8.6. Молекула оксида кремния
Мы можем рассматривать образование атомной структуры всех химических элементов, присутствующих в таблице Менделеева. Однако нас будет больше интересовать атомы и молекулы окружающей нас природы. Как мы знаем, в земной коре большом количестве присутствуют кислород, кремний, алюминий и железо. Чем обусловлено такое их обилие, мы проанализировали. Теперь посмотрим, в составе каких молекул и кристаллов они генерировались.

Рис. 8-19. Выборочные данные о среднем составе земной коры по А.Е. Ферсману (вес.%)
В первую очередь рассмотрим силикаты и алюмосиликаты, в состав которых входит молекула оксида кремния. Силикаты составляют примерно 75 процентов земной коры. Такое обилие силикатов на Земле должно быть обусловлено тем, что последний этап дифференциации хронооболочек планеты завершился структурой пространства, наиболее способствующему их образованию.
Посмотрим, как может выглядеть голограмма оксида кремния. Как было видно из предыдущих примеров, матрицы могут продуцировать как отдельные атомы, так и молекулы, и элементы кристаллов. Атомный номер кремния 14, поэтому его голограмма состоит из 14 сфер. На рис.8-20 показана плотная упаковка. Атомный номер кислорода 8. Упаковка восьми сфер самая простая и соответствует кубу, в каждом углу которого находится сфера. Если сравнить с решетками Браве, то видно, что они представляют собой два из 4-х основных типов плотной упаковки.

Рис.8-20. Голограммы атомов кремния и кислорода. Кремний – гексаэдр, вписанный в октаэдр. Кислород – октаэдр.
Главным структурным элементом, как твердого диоксида кремния, так и всех силикатов выступает группа [SiO4/2], в которой атом кремния Si окружен тетраэдром из четырёх атомов кислорода О. При этом каждый атом кислорода соединен с двумя атомами кремния. Фрагменты [SiO4/2] могут быть связаны между собой по-разному. Среди силикатов по характеру связи в них фрагментов [SiO4/2] выделяют островные, цепочечные, ленточные, слоистые, каркасные и другие (рис.8-26).
Если выделить фрагмент тетраэдра оксида кремния, то он выглядит также как молекула метана, но внутреннее строение хронооболочек разное.

Рис. 8-18. Атом кремния окружен тетраэдром, состоящим из четырёх атомов кислорода

Рис.8-21. Общая голограмма молекулы кремнезема
На рис показана голограмма молекулы кремнезема. Она представлена несколькими конфигурациями: общая – это тетраэдр, кремний – гексаэдр, вписанный в октаэдр, кислород – четыре октаэдра. Примерно так выглядел последний этап квантования хронооболочек на периферийных участках Земли. Внутри были более сложные конструкции. Такая конструкция внутренних хронооболочек будет генерировать в своем общем центре молекулы кремнезема, которые в зависимости от внешних хронооболочек будут создавать различные кристаллические структуры. Таким образом, кристаллическая структура, образуемая в различных силикатах кремнекислородными радикалами, будет определяться внешней структурой молекул, т.е. их голографическими моделями.

Рис.8-10. Образование различных топологий внутреннего пространства
На рис.8-10 показаны два варианта квантования хронооболочек с образованием разных топологий внутреннего пространства. Каждая из сфер – это хронооболочка, которая образует две волны, одна из них расходящаяся образует внутренне пространство планеты, а другая – сходящаяся начинает продуцировать корпускулы – атомы и молекулы.
8.7. Алюмосиликаты
Снова возвращаемся к алюмосиликатам. Как устроены голограммы силикатов нам понятно. Алюмосиликаты возникают из тех же модулей, что силикаты, только структура их хронооболочек немного меняется. Для кремния голограмма представляет собой гексаэдр, включенный в октаэдр, что дает 14 протонов в атоме. Алюминий, атомный номер которого 13, также имеет энергетически выгодную плотную упаковку. Однако она представляет собой додекаэдр, образованного 12-ю хронооболочками, в центре которого находится еще одна 13-я хронооболочка. Поэтому, когда в силикатах происходит замена центрального атома кремния на атом алюминия, то такая структура за счет своего низкоэнергетического состояния также приобретает право на существование в широких пределах.
Отметим также, что железо также генерируется примерно таким же составом голограмм. Атомный номер железа 26 говорит о том, что его голограмма представлена гексаэдром (6), октаэдром (8) и додекаэдром (12). Три структуры позволяют разместить 26= 6+8+12 протонов в энергетически выгодную конструкцию с низкой энтропией. Надо сказать, что широкая распространенность этих 4-х химических элементов в Солнечной системе связана с тем, что в образовании голограмм их хронооболочек лежат правильные многогранники, которые обладают не только низким уровнем энтропии, но также и низким уровнем потенциальной энергии.
Алюмосиликаты широко распространены в природе, они составляют до 50% массы земной коры. Это полевые шпаты, фельдшпатиды, слюды и другие. Термин «алюмосиликаты» был введен в минералогию Вернадским, впервые правильно оценившим роль алюминия в построении минералов. Обобщив огромный фактический материал по каолинам, слюдам и другим минералам, Вернадский разработал и выдвинул теорию строения алюмосиликатов в виде теории каолинового, или слюдяного, ядра. Согласно этой теории в основе строения алюмосиликатов лежит общее для этих минералов каолиновое ядро, в состав которого входят два атома алюминия, два атома кремния и семь атомов кислорода. В. И. Вернадский рассматривал полевые шпаты, слюды и другие алюмосиликаты как соли алюмокремнёвой кислоты, т. е. как продукты присоединения к указанному ядру ряда элементов-катионов: натрия, калия, кальция и других.
В последствии рентгеноструктурные исследования силикатов и алюмосиликатов показали, что основным «строительным кирпичиком» этих соединений является атом кремния или алюминия, окруженный четырьмя атомами кислорода, – кремне(алюмо)кислородный тетраэдр SiO4(AlO4). Многообразие же алюмосиликатов объясняется разными способами соединения этих тетраэдров, которые обычно сочленяются вершинами с образованием связей Si-O-Si и Si-O-Al (рис. 22).

Рис. 22. Способы соединения кремне(алюмо)кислородных тетраэдров: а) отдельный тетраэдр, б) два тетраэдра с общей вершиной, в) фрагмент простой цепи, г) фрагмент «ленты», д) фрагмент «листа».
Сайт http://encyclopaedia.biga.ru/enc/science_and_technology/ALYUMOSILIKATI.html
Как считает Е.Савинкина, у каркасных алюмосиликатов имеется непрерывный трехмерный каркас из тетраэдров, объединенных общими вершинами. Случаи связывания гранью или ребром неизвестны. Все атомы кислорода у тетраэдров кремния и алюминия являются общими. Так как в целом соединение должно быть электронейтральным, то полости между полиэдрами дополнительно заполняются катионами, которые нейтрализуют отрицательный заряд каркаса, возникающий при замене кремния на алюминий. К природным алюмосиликатам относятся, в первую очередь, полевые шпаты, имеющие каркасную структуру (например, ортоклаз NaAlS3O8, альбит NaAlSi3O8, анортит CaAl2Si2O8).
В XVIII веке были открыты цеолиты – каркасные алюмосиликаты, состав которых можно описать общей формулой MIxMIIy(Alx+2ySizO2x+4y+2z)·nH2O. Свое название они получили от греческих слов zeo – киплю и lithos – камень, т.к. образуют пузырчатое стекло при сильном и быстром нагревании. Известно более 40 минеральных видов природных цеолитов. С 1950-х в промышленных масштабах производятся искусственные цеолиты. В лабораториях синтезировано более 100 структурных видов, большинство которых не имеют природных аналогов.
Для нас цеолиты интересны тем, что показывают, какие еще виды пространств могут образоваться из хронооболочек. Цеолиты – это нестехиометрические соединения, их составы изменяются в широких пределах, образуя ряды твердых растворов. Кристаллические структуры цеолитов состоят из тетраэдров [SiO4]4– и [АlO4]5–, соединенных вершинами в ажурные каркасы, в полостях и каналах которых находятся катионы металлов и молекулы Н2О. Они характеризуются рыхлой структурой с широкими каналами (рис. 23).

Рис. 23. Типичные цеолиты, образованные содалитовыми блоками (срезанными октаэдрами): а – синтетический цеолит состава Na12(Al12Si12O48).27H2O (ширина канала 420 пм); б – фожазит Na12Ca12Mg12Al59Si133O384.235H2O (ширина канала 740 пм).
Сайт http://encyclopaedia.biga.ru/enc/science_and_technology/ALYUMOSILIKATI.html
В слоистых алюмосиликатах кремне- и алюмокислородные тетраэдры соединены в одной плоскости в непрерывный слой. Слои тетраэдров обособлены друг от друга. Связь между слоями обеспечивается ван-дер-ваальсовыми силами или силами электростатического притяжения с помощью катионов, нейтрализующих отрицательные заряды слоев. Из-за наличия слоев тетраэдров и слабых связей между ними слоистые алюмосиликаты образуют чешуйчатые, листовые или таблитчатые агрегаты.
К слоистым алюмосиликатам относятся некоторые глинистые минералы, например галлуазит (H2O)4[Al2(Si2O5)(OH)4]. Все такие минералы содержат между слоями решетки молекулы воды. В некоторых из них, например, вермикулите (Ca,Mg)0,7(Mg,FeIII,Al)6(Al,Si)8O20·8H2O, вода быстро удаляется при нагревании, и минерал расслаивается. Обезвоженный вермикулит применяют в качестве легкого наполнителя при изготовлении бумаги, пластиков и красок, а также как упаковочный материал.
Минералы группы слюд образуют слоистую решетку с ионами «гостей» между силикатными листами «хозяина» (рис. 24).

Рис. 24. Минералы группы слюд на примере мусковита KAl2[AlSi3O10](OH)2 (показано два повторяющихся блока решетки)
Сайт http://encyclopaedia.biga.ru/enc/science_and_technology/ALYUMOSILIKATI.html
Слюды легко расщепляются на очень тонкие, гибкие и в то же время упругие пластинки. Они обладают высокими диэлектрическими свойствами и огнестойкостью. В виде тонких пластин они прозрачны, поэтому было время, когда их использовали в качестве оконного стекла.
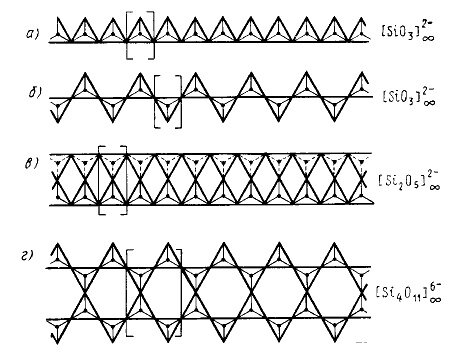
Рис. 25. Некоторые типы цепочечных и ленточных кремнекислородных радикалов бесконечных размеров

Рис.26. Кремнекислородные радикалы в различных силикатах: а, б, в, г – островные структуры; д – цепи; е – ленты; ж – слоистая структура.
Дальнейшее построение голограмм для каждой группы кремнекислородных радикалов поможет лучше понять многообразие различных форм в образовании кристаллов силикатов. Потому что основную и определяющую роль в образовании кристаллических форм играет влияние внешней структуры, которая обусловлена голограммой молекул.
8.8. Принцип Кюри
Основная идея, которая заключена в голографических структурах молекул, состоит в том, что при определенных условиях, например, в расплавах или насыщенных растворах, рост кристаллов будет всегда осуществляться в неизменном виде. Информация об их структуре содержится в голографической форме записи. Разные модификации кристаллических структур буду определяться внешними условиями, другими словами, они зависят от формы внешнего пространства. Т.к. структура внешнего пространства накладывает свои особенности на структуру внутреннего. Этот принцип мы сформулируем так: «Симметрия причин сохраняется в симметрии следствий».
Впервые этот принцип сформулировал Пьер Кюри в 1894 году для образования кристаллов в зависимости от внешних условий. Он его сформулировал так: объект сохраняет лишь те элементы симметрии, которые совпадают с элементами симметрии окружающей (питающей) среды. В случае равномерного питания со всех сторон - симметрия среды = симметрия шара, кристалл сохраняет все присущие этому минералу элементы симметрии. Кристалл вырастает в виде правильного многогранника, соответствующего истинным простым формам.
Если кристалл растет на горизонтальной поверхности в спокойных условиях, то вокруг него создаются расположенные вертикально концентрационные потоки. В этом случае среда имеет симметрию конуса. Такие кристаллы сохраняют только одну ось симметрии n порядка и соответствующее число плоскостей симметрии, если эти элементы симметрии кристалла совпадут с таковыми среды. При случайной ориентировке зародыша на горизонтальной поверхности вырастает кристалл вообще без элементов симметрии.
При росте кристаллов в движущемся потоке вещества, который имеет единственную плоскость симметрии, разрастание кристаллов идет навстречу потоку; если плоскость симметрии кристалла - затравки совпадает с плоскостью симметрии потока, то она сохраняется и в наросшей части кристалла. В случае несовпадения плоскостей симметрии выросший кристалл будет вообще лишен видимой симметрии. Влияние симметрии среды зависит от типа движения, от характера завихрений. Если скорость потока мала и вихри не отрываются от растущего кристалла, задние грани слабо омываются и голодают, в них образуются включения. Если скорость движения очень велика, то вихри быстро сносятся с поверхности растущего кристалла, пересыщение в объёме вихря мало меняется, все грани растут равномерно - идет бездефектный рост. Время стационарного состояния вихрей прямо зависит от вязкости раствора и обратно пропорционально размеру кристалла и скорости потока. Во всех случаях, кроме изометрической среды питания, образующиеся кристаллы будут обладать ложными габитусными формами, т.е. искаженной внешней симметрией. По ассиметрично выросшим кристаллам можно определять направление движения питающего палеопотока.



























