|

Голографическая модель Вселенной.
Книга 3. Происхождение материи
4. Первый уровень реальности.
Происхождение материи. Внутренний вакуум
Проанализировав образование физического вакуума на предельном уровне квантования хронооболочек, мы видели, как образуется возможность существования материи в непроявленном состоянии. Такой физический вакуум относится к нулевому уровню реальности и соответствует голографической картине мира. Именно здесь происходит окончание дифференциальных процессов или квантования хронооболочек. Следующий уровень реальности – первый – соответствует процессам интеграции (или интерференции) хронооболочек, в результате которой появляется материя.
Однако самое интересное заключается в том, что рассматривая процесс интеграции, мы снова будем говорить о дифференциации. Происходит это потому, что процесс интерференции, как было показано выше, представляет собой такое перераспределение потоков энергии в пространстве, при котором внутри пространства возникает структура. Она состоит из чередований энергетических максимумов и минимумов. Благодаря этим максимумам и минимумам и возникает материя. Причем возникают две противоположные материальные сущности, одну из них назовем волновой формой материи, а другую корпускулярной. Понятно, что корпускулам соответствуют исключительно области максимумов, тогда как все остальное пространство заполнено просто волнами. Следовательно, интеграция или сложение хронооболочек теперь определяется процессами дифференциации по корпускулярно-волновому признаку.
То же самое объяснение можно предложить и в другом виде. Если дифференциация пространства до нулевого порога осуществлялась в положительной области допустимых значений, то за нулевым порогом дифференциация переходит в область своих отрицательных значений, что соответствует понятию антидифференциации. Чтобы определить понятие антидифференциации воспользуемся обычной заменой функции на ее антифункцию. Тогда понятию антидифференциации будет соответствовать понятие интегрирования или интеграции. Здесь дальнейший процесс дифференциации пространства заменяется на интеграционный процесс образования материи, т.к. антидифференциация есть процесс дифференцирования уже не пространства, а его содержимого, т.е. выделяющейся энергии динамического хаоса. Сделав такое допущение, мы снова вернулись к основному положению, что любая дифференциация заканчивается интеграцией, только теперь хотелось лишний раз подчеркнуть, что интеграция это тот же процесс, который продолжает дифференциацию, но на качественно ином уровне.
Поэтому в отличие от нулевого уровня первый уровень реальности имеет более сложный дифференцированный вид, и представляет собой семь подуровней интеграции. Это означает, что первый уровень реальности разбивается еще на семь подуровней, каждый из которых назовем вакуумом первого, второго, третьего и т.д. рода. Почему именно вакуумом? Потому что, анализируя несопоставимость вещества и вакуума, мы уже пришли к выводу, что вещество является редчайшим исключением в огромном пространстве, заполненном субстанцией вакуума. Поэтому есть ли смысл говорить о материальных уровнях, если практически все пространство состоит из пустоты, что внутри вещества, что в космосе.
4.1. Структура физического вакуума нулевого рода
Образование вакуума внутри вещества происходит при возникновении материи из ее непроявленного состояния. Рассмотрим, как образуется самый первый в мире атом – атом водорода, и покажем, что дешифратором в голограмме мира является поток времени точно так же, как луч света является дешифратором объемного изображения голограммы.
Вещество, как говорилось выше, образуется вместе с пространством за счет преобразования времени на нижнем предельном уровне квантования хронооболочек. Теперь время можно рассматривать как сущность, которая находится по разные стороны от момента настоящего. Поэтому в будущем мы можем представить его в виде потока энергии, а в прошлом – в виде пространства-материи. Проходя через точку «настоящего» время преобразуется. Точка «настоящего» - это точка причины, через которую время втекает к следствию. Ранее мы уже установили, что в природе не существует нулей и бесконечностей. Поэтому точка причины L=0 (или источник) представляет собой очень маленький контур конечных размеров, который ограничивает внутри себя замкнутую поверхность. В таком виде эта «точка» была названа гравитационным диполем в свернутом состоянии (подробнее см. «Поговорим о пространстве» http://merkab.narod.ru/). В этом смысле наш гравитационный диполь можно сопоставить с элементарной петлей в теории петлевой квантовой гравитации.
Энергия – время, поступая из точки причины L=0 в точку следствия L=1, преобразуется в вещество и пространство с определенной скоростью с2. Можно сказать, что вещество поступает в подсистему через положительную поверхность двухмерного объекта, а пространство - через отрицательную. Вещество и пространство появляются одновременно как две противоположности, отрицающие и дополняющие друг друга.
Для тех, кого интересует математическая сторона вопроса, это уникальное событие можно описать и в виде формул. Как уже было сказано, бегущих волн времени не существует потому, что время всюду появляется сразу. Но рассматривая преобразование причин в следствие, мы можем говорить о волнах преобразования времени в материю и пространство. Поэтому воспользуемся формулами волнового уравнения.
Как известно, для однородного одномерного волнового уравнения, которое описывает распространение бегущей волны с фазовой скоростью ν вдоль оси х,
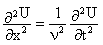 (4)
(4)
решением является функция вида (F1 и F2 – произвольные дважды непрерывно дифференцируемые функции)4
4- Параметр t, как говорилось выше, представляет собой не время, а продолжительность одного цикла Т, т.е. 0 < t < T, обусловленного скоростью протекания процессов или ходом времени. Для постинтегральных систем параметр t определяется по формуле t= nT , где n – целые числа, обозначающие количество циклов.
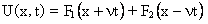 ( 5)
( 5)
В нашем случае мы имеем дело с трехмерными сферическими волнами. Поэтому рассмотрим частный случай трехмерного волнового уравнения, решением которого являются сферические волны (Богачков И. В., 2001). Для сферической функции F(r)
(F(r) имеет только радиальную составляющую,
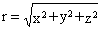 ). ).
После замены переменных в (4) получаем одномерное уравнение относительно r:
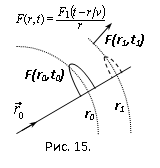
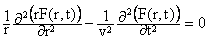 (6)
(6)
Умножив (6) на r, мы получим уравнение вида (4) относительно функции r F(r):
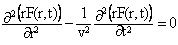 , решение которого известно – (5):
, решение которого известно – (5):
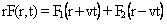
, откуда следует:
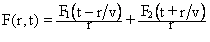 (7)
(7)
Первое слагаемое (7) представляет собой сферическую волну, расходящуюся от источника (рис.15). Второе слагаемое, если следовать указаниям Фейнмана, надо отбросить, поскольку волна, движущаяся внутрь источника, физического смысла не имеет. Хоть уравнения Максвелла предоставляют обеим волнам равные возможности, обычно привлекается без какого-либо доказательства тот факт, что «физическим смыслом» обладает только расходящаяся волна.
Однако в нашем случае сходящаяся волна имеет физический смысл, причем достаточно серьезный, т.к. именно она определяет корпускулярные свойства волны. Таким образом, второе слагаемое представляет собой сферическую волну, движущуюся внутрь источника. Т.е. мы видим, что у нас образуются две волны, одна из которых устремляется к центру контура-петли, а другая - наружу. В нашем случае фазовой скоростью является скорость преобразования энергии ν=с2. В таком виде мы опять получаем квантование энергии на два вращающихся потока или две волны. Физический смысл этих волн очевиден, одна из них представляет собой расходящуюся сферу вакуума, окружающую материю. Сходящаяся волна, та, что движется к центру контура, представляет собой организацию самой материи, т.е. вещества. Отметим, что бегущая волна энергию переносит. Поэтому часть энергии переносится к границе кварта, а часть к его центру.
Несколько слов можно сказать по поводу физического смысла. Если бы в своё время Поль Дирак не задумался о значении второго решения волнового уравнения при введении в него преобразований Лоренца, и не предположил бы, что отрицательное решение описывает гипотетическую частицу, объяснил бы его как просто мнимое, не имеющее физического смысла, то вероятно экспериментально позитрон был бы открыт много позже. (Зныкин П.А.2008)
Теперь поговорим подробнее о каждой из этих волн. Вначале рассмотрим ту волну преобразования, что движется наружу и образует вакуум, т.е. расходящуюся волну, которую можно представить в таком виде, как изображено на рис.16.
Воспользуемся математическим уравнением амплитуды сферической волны (8), которая, как известно, уменьшается при удалении от источника как 1/r (мощность соответственно как 1/r2). Это связано с тем, что мощность изотропного источника (Pист) равномерно распределяется по расходящимся сферам. С учетом того, что площадь сферы 4πr2 получаем :
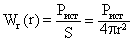 (8)
(8)

Рис. 16. Расходящаяся волна
Очевидно, что даже при отсутствии потерь в пространстве плотность потока мощности W(r) сферической волны уменьшается с расстоянием как 1/r2. Такое представление об уменьшении плотности потока мощности показывает нам, что распространение волны в виде сферы вакуума не беспредельно, а имеет свои границы. Следовательно, образующееся пространство также ограничено. И поскольку нашу сферическую волну мы представляем в виде стоячей волны, то энергия второго потока перераспределяется к внешней границе пространства, образуя непроницаемый барьер в виде сил отталкивания (см. выше явление интерференции).
Теперь о сходящихся волнах. Вначале покажем, как они реализуются. Такая реализация также возникает при интерференции волн. В связи с тем, что происходит квантование хронооболочек, то энергия поступает в систему не непрерывным потоком, а дискретно, т.е. квантами. Понятно, что минимальный квант определяется минимальной образующейся подсистемой. Теперь посмотрим, как преобразуется интерференционная картина в сходящуюся волну. Не вдаваясь в теоретические расчеты, мы геометрическим способом построим сходящуюся волну на основе тех же двух источников волн (рис.16-2), попеременно закрашивая дуги полуокружностей обеих волн. Как видно из построения, результат у нас получается в виде спирали (рис.16-2 В). Поскольку мы знаем, что при интерференции энергия волн перераспределяется в пространстве, то можем предположить, что в сходящейся волне энергия двигается внутрь источника по спирали.

Рис.16-2. Геометрическое построение сходящейся волны при интерференции двух волн (хронооболочек)
Более точный результат интерференции сходящихся волн получается в виде полуспиралей. Как, например, при образовании голограммы протона или атома водорода, где стрелочками показано направление энергии
Сформулирую эту мысль еще раз: часть энергии остается в системе, но перераспределяется в пространстве к внешней границе, а другая часть перераспределяется к центру или в точку следствия и попадает в подсистему. Ранее говорилось, что, с точки зрения системы та часть, что попадает в подсистему, оказывается в нелокализованном состоянии. Другая часть, что осталась в системе, находится в локализованном состоянии. Поэтому преобразование хронооболочек мы также можем рассматривать как разделение энергии, на два потока. Причем тот, который локализовался, представляет собой волновую (или полевую) форму материи, а другой – нелокальный – корпускулярную материю.
Таким образом, мы подошли к окончательному понимаю того, как образуется гравитационный веерный диполь, имеющий в центре материальную составляющую в виде гравитирующей массы, и окружающую ее сферу вакуума, обладающую силами антигравитации. С другой стороны мы еще раз увидели, что пространство не существует вечно, оно рождается одновременно с каждым материальным объектом.
дальше
Наверх
на главную
|