Голографическая модель Вселенной. Новая концепция мироздания. Принципы самоорганизации материи

1.Шестигранные колонны
       1.1.Дорога гигантов (Giants Causeway), Ирландия
       1.2.Чертова башня или Дэвилс Тауэр (Дакота, США)
       1.3.Каменный город Нан-Мадол
       1.4.Фингалова пещера
       1.5.Выходы базальта в Калифорнии
       1.6.Курильские острова. Мыс Столбчатый
       1.7.Украина. Заказник «Базальтовые столбы»
       1.8.Армения. Ущелье Гарни
       1.9.Происхождение шестигранных столбов
2. Порядок из хаоса
       2.1.Ячейки Бенара
       2.2.Химическая реакция Белоусова-Жаботинского
       2.3.Фигуры Хладни
       2.4.Эксперименты Йенни
       2.5.Как образуются снежинки?
       2.6.Круги на полях
3. Второе начало термодинамики
       3.1.Динамическая энергия
       3.2.Структурообразующая роль времени
4. Объяснение процессов самоорганизации
5. Заключение

В основе образования нашей Вселенной лежит важнейший принцип самоорганизации материи. В науке изучение такой самоорганизации началось совсем недавно. Считается, что природе имманентно[1] присущ характер самоорганизации, поскольку мы повсеместно видим, что простое вещество организуется в сложное на примере атомов, молекул, живых систем, галактик. Однако природа такой самоорганизации научного объяснения пока не получила.

Тем не менее, как мы видим, в природе принцип самоорганизации материи является основополагающим, более того, он проявляется себя на всех уровнях организации материи. Но если такую организацию на примере живого вещества мы видим повсеместно, то для неживой материи самоорганизация далеко не столь очевидна. Поэтому в этой статье мне хотелось бы показать несколько удивительных природных феноменов такой самоорганизации. Не только показать, но и дать объяснение их происхождению с точки зрения голографической модели. Потому что официальная наука ничего сказать по этому поводу не может.

В данной статье мы рассмотрим такие удивительные природные явления, когда из неорганизованной хаотичной материи возникают структуры, обладающие упорядоченностью и правильной геометрической формой. К таким явлениям относятся известные шестигранные колонны, встречающиеся в разных местах на нашей планете. Проанализируем результаты некоторых экспериментов, которые позволяют увидеть, как из хаоса возникает порядок. Это конвективные ячейки Бенара и фигуры Хладни. Получим, наконец, ответ на вопрос, как появляются снежинки, обладающие столь изящной геометрической формой. Еще раз обратимся к такому явлению, как круги на полях, которые, на мой взгляд, имеют вполне естественное происхождение. Потому что в их образовании опять же участвует все тот же природный феномен, который организует порядок из хаоса. И в завершение определим, какие природные силы являются созидающими, т.е. то, что превращают простое вещество в сложное, а какие силы, наоборот, разрушающими.

1.Шестигранные колонны

В некоторых местах нашей планеты наблюдаются странные структуры. Это огромные колонны шестигранной формы естественного происхождения. Одно из таких мест находится в Ирландии и известно как Дорога гигантов, другое в Вайоминге – это Чертова башня или Башня Дьявола, еще есть Фингалова пещера (Шотландия), Ущелье Garni (Армения), Призмы Базальта (Мексика), "органные трубы" – образование на горе Cargill в Новой Зеландии. Все они хорошо известны тем, что образуют столбчатые геологические отдельности в виде шестигранных колонн.

1.1. Дорога гигантов (Giants Causeway), Ирландия

На северо-востоке Северной Ирландии находится удивительное природное образование, которое называют Дорогой гигантов. Эта территория покрыта 40 тысячами базальтовых колонн правильной формы. Большинство колонн, составляющий массив, шестиугольные, но есть колонны с 4, 5, 7 и 8 гранями. Самая высокая из них в высоту достигает 12 метров, а толщина застывшей лавы вокруг – до 28 метров. В 2005 году по опросам издания Times, Дорога гигантов была названа четвертым чудом света на территории Великобритании.

Рис.1.2 Большинство колонн, составляющий массив, с шестиугольными гранями.

Выходы базальта в Бушмилсе (Северная Ирландия). Для обнажений базальтов характерна шестигранно-призматическая (столбчатая) отдельность, нормальная к поверхности лавового покрова (обычно вертикальная, напоминающая колоннаду) или к контактам даек (в случае их крутого залегания – субгоризонтальная, похожая на дровяную поленницу).

Базальты легко опознаются по столбчатой отдельности, которая выглядит весьма эффектно: столбы могут достигать огромных размеров. Торцовая поверхность базальтовых покровов, разбитых трещинами призматической отдельности, производит впечатление «мостовой гигантов» вымощенной громадной фигурной брусчаткой.

1.2. Чертова башня или Дэвилс Тауэр (Дакота, США)

В Соединенных Штатах Армерики в штате Вайоминг прямо среди Великих Равнин высится загадочная гора, которую называют Башней Дьявола. Это столбчатая отдельность высотой 390 м, возникшая 200 миллионов лет назад. В чем же ее загадочность? Прежде всего, в ее необычном облике. Гора похожа то ли на какой-то громадный пень, то ли на могучую крепостную башню, в которой отдельные каменные столбы сложили в пучок. У этой горы необычайно правильная форма, настолько правильная, что трудно поверить в естественность ее происхождения.

Но кроме своего облика, Башня Дьявола всегда интриговала человека нелогичностью своего появления среди равнин, которые раскинулись тут не на одну сотню километров. И больше ни одной скалы вокруг. Такие горы еще называют геологическими отдельностями. По предположениям ученых гигантская базальтовая скала в форме ребристого усеченного конуса возникла около двухсот миллионов лет тому назад. Ее высота составляет около четырехсот метров, а диаметр скалы в основании триста метров, а на вершине – восемьдесят метров.

Вполне естественно, что в древние времена, а иногда и в наши дни, для местных жителей скала была идолом, которому следовало поклоняться, а многие даже боялись долго стоять рядом с Башней Дьявола, потому что на самой вершине скалы не раз видели странное и необъяснимое свечение.

Правильность формы скалы наталкивала местное население на мысль об искусственности ее сооружения, но с другой стороны было ясно, что человек в древние времена не мог возвести подобный монумент, который затмевал собой даже египетские пирамиды. Поэтому люди приписали авторство башни самому Дьяволу. Местное индейское население верило, что на самой вершине скалы и живет этот дьявол. Когда дьявол злился на людей или хотел их наказать, он устраивал пляски под барабанный бой, который вызывал гром и молнии. Небо закрывалось черными тучами, а огненные стрелы поражали людей, и спрятаться от них не было никакой возможности.

Бледнолицые переселенцы, пришедшие в Америку, услышали от индейцев эту легенду и назвали гору выразительным именем Дэвилс-Тауэр, что означает Башня Дьявола. С тех пор родилось множество легенд и преданий, как об этой скале, так и о происходящих здесь событиях.

Так как Башня Дьявола среди окружающих равнин самый высокий объект данной местности, то молнии, в самом деле, очень часто попадают именно в ее вершину. Нередко здесь наблюдаются и загадочные световые аномалии. Все это среди любителей непознанного и уфологов породило гипотезу о том, что плоская вершина скалы – это космодром для посадки НЛО.

Такая гипотеза в сочетании с экзотической природой естественно не могла оставить равнодушными современных голливудских кинематографистов, приверженцев мистики и фантастики. Именно здесь родился фантастический триллер Стивена Спилберга под названием «Близкие контакты третьей стeпeни», в котором инопланетный космический корабль приземляется прямо на посадочной площадке, расположенной на вершине Башни Дьявола.

Рис. 2.1. В Соединенных Штатах Армерики в штате Вайоминг прямо среди Великих Равнин высится загадочная гора, которую называют Башней Дьявола

Хотя высота Башни Дьявола относительно небольшая, но скала пользуется дурной славой среди альпинистов. Стены Башни очень отвесные, поэтому забраться на нее достаточно трудно, но еще тяжелее спуститься обратно. Скала отличается неприступностью. За всю историю альпинизма даже бывалые альпинисты, оснащенные специальным снаряжением, предпринимали всего три попытки покорить Башню дьявола.

Первым, кому удалось это сделать, был некий местный житель еще в девятнадцатом веке. Вторую удачную попытку покорить Башню Дьявола в одиночку осуществил Джек Дюрранс в 1938 году. Много лет спустя, уже достаточно пожилой Дюрранс был вынужден покорить вершину еще раз. Ему пришлось с группой альпинистов-спасателей снимать со скалы парашютиста, который приземлился на ее вершину.

Джордж Хопкинс был опытным парашютистом и захотел приобрести мировую известность, приземлившись с парашютом на вершину Башни Дьявола. Таким образом, он решил стать третьим покорителем неприступной скалы, правда, с воздуха.

Хопкинса предупреждали, что такой прыжок очень опасен, но он явно переоценив свои возможности, все-таки совершил его. Парашютист приземлился довольно удачно на вершину скалы, правильно все рассчитав, но, судя по всему мужчина не учел, что со скалы еще придется и спускаться, а парашют в этом деле ему помочь не мог. Так Хопкинс в течение нескольких дней был самым известным пленником Башни Дьявола.

Спуститься сам вниз Хопкинс не мог. Никакой самолет на такую маленькую площадку сесть не смог бы. Места для посадки хватило бы вертолету, но тут возникала другая неразрешимая проблема – постоянно дующий на вершине скалы ураганный ветер, в полном смысле слова, сдувал все вертолеты, подлетающие к вершине Башни. Спасатели пытались вбрасывать парашютисту с вертолетов и самолетов веревки и веревочные лестницы, надеясь с их помощью спасти беднягу, но те под воздействием сильного ветра, разбивались о камни и были непригодны для спуска.

После нескольких неудачных попыток спасения Хопкинса, стало понятно, что помочь в этой ситуации сможет только профессиональный скалолаз. Два известных скалолаза Горрел и Филд несколько часов пытались покорить неприступную Башню Дьявола, но, все же отступили, признав, что это им не по силам.

А в это время самолеты кружились над вершиной скалы и сбрасывали Хопкинсу продукты, теплые вещи и различное оборудование, присланное различными компаниями в качестве рекламы. Однако изобилие еды и одежды не придавало сил и энтузиазма пленнику. А в придачу ко всем бедам обнаружилось еще, что на неприступной гладкой гранитной скале обитают целые полчища голодных крыс, которые наглели с каждым часом все больше и больше. Как они сюда забрались и чем питаются, было совершенно непонятно.

Все СМИ Америки кинулись на поиски Дюрранса, единственного живого покорителя скалы. Был создан специальный комитет по спасению парашютиста. Через сутки нашелся Дюрранс, живший в Дармуте. Еще сутки альпинисту понадобились для того, чтобы добраться на место происшествия и начать приготовления для восхождения группы спасателей. Группа совершала восхождение по маршруту, который знал только Дюранс. Неприятным сюрпризом стал еще и густой туман, окутавший скалу. Но, мужественно преодолев все препятствия, альпинисты во главе с Дюрансом все же забрались на вершину Башни Дьявола.

Несчастный, обессилевший от ветра и борьбы с крысами парашютист, был помещен в специальную альпинистскую люльку и удачно спущен со скалы на землю. Почти неделю Хопкинс был в плену у дьявольской Башни.

Действительно, невероятная дьявольская скала. Альпинистам покоряются горы, высота которых превышает восемь тысяч метров! А тут меньше четырехсот метров, и полное всеобщее бессилие! Какие же тайны и загадки скрывает в себе Башня Дьявола, если не хочет открываться для людей? Возможно, когда-то мы их и разгадаем.

Интересно происхождение и геология этой геологической отдельности из базальта под названием Башня Дьявола. Примерно двести миллионов лет тому назад территория нынешней Великой Равнины была покрыта морем. Дно этого моря представляло собой мощную толщу осадков песчаников, сланцев и известняков. В одном месте на дне моря произошло внедрение в эту толщу расплавленной магматической массы из недр земли. После застывания магмы, из нее образовалось столбообразное базальтовое тело, называемое в науке штоком.

Шли годы, века, тысячелетия, море постепенно отступало, мягкие осадочные породы разрушались, а через миллионы лет, образовавшийся огромный шток оказался полностью на суше. Когда базальт скалы постепенно остывал, то он приобрел форму живописных вертикальных шестигранных столбов.

Рис.2.3. Основа, представляющая собой высоченный каменный цилиндр, кажущийся издалека таинственным каменным снопом, в состав которого входят базальтовые каменные колосья, по сей день величественно красуется, приковывая к себе всеобщие взгляды, и является уникальным зрелищем

Время, эрозия и атмосферные явления постепенно разрушало даже такую прочную породу как базальт. От вершины скалы отделялись и падали к основанию куски породы, что со временем привело к образованию пологого холма у подножия. Однако основа, представляющая собой высоченный каменный цилиндр, кажущийся издалека таинственным каменным снопом, в состав которого входят базальтовые каменные колосья, по сей день величественно красуется, приковывая к себе всеобщие взгляды, и является уникальным зрелищем.

1.3. Каменный город Нан-Мадол

Среди бесчисленных микронезийских островов, рассеянных в Тихом океане между экватором и Тропиком Рака есть один очень удивительный остров – Понапе, расположенный в восточной части Каролинских островов. Он вулканического происхождения, окружен почти непрерывным коралловым рифом, в котором имеется несколько проходов к открытому морю. Понапе имеет размеры не более 20 километров и вполне мог бы уместиться в пределах Московской кольцевой автодороги. Его внутренняя часть, круто поднимающаяся по направлению к нескольким горам высотой около 800 метров, густо покрыта тропическим лесом, а берега – мангровыми зарослями.

Остров интересен тем, что на нем расположен каменный город Нан-Мадол. Это комплекс очень древних сооружений, сложенный из каменных брусьев до удивления похожих на наши шестигранные колонны. На строительство этого города без окон и дверей, ушло 250 миллионов тонн базальта, что по объему строительства сопоставимо с Великой пирамидой в Египте. Некоторые базальтовые балки по габаритам и массе больше любого из двух миллионов блоков в пирамиде Хеопса. Нан-Мадол давным-давно заброшен, его стены, проглядывая сквозь густые мангровые заросли, наводят суеверный ужас на тех людей, что ныне живут поблизости.

Ближайшие современные разработки базальта находятся на северном берегу Понапе – почти на противоположной от Нан-Мадола стороне острова, и, судя по всем имеющимся у археологов данным, базальтовые колонны доставлялись именно оттуда. Мне этот пример показался удивительный тем, что шестигранные колонны, которые сотворила природа, были использованы древними людьми для своих строительных нужд.

Рис. 3.2. Этот комплекс очень древних сооружений сложен из каменных брусьев

Фингалова пещера

Еще одно природное сооружение, состоящее из шестигранных колонн, находится недалеко от Дороги гигантов и называется Фингалова пещера (англ. Fingal’s Cave) – прославленная морская пещера, вымытая в скале морской водой, на острове Стаффа.

Остров Стаффа – один из Внутренних Гебридских островов, лежащих у Шотландского побережья Соединенного Королевства. Весь остров состоит из выстроившихся вплотную друг к другу колонн правильной формы, от трех- до восьмигранных, чаще же всего – шестигранных. Открыта пещера была в 1772 году, и с тех пор каждый уважающий себя путешественник считает своим долгом при поездке в Шотландию наведаться сюда.

Рис.4.1 Фингалова пещера – прославленная морская пещера, вымытая в скале морской водой, на острове Стаффа, входящем в группу Внутренних Гебридских островов.

Рис.4.2.Фингалова пещера с сайта http://muz4in.net/news/ostrov_staffa/2011-02-02-15371

Рис.4.3. Такую удивительную шестигранную форму колонн здесь можно наблюдать

Выходы базальта в Чехии

Рис.4.Панская скала у Каменицки-Шенова, северная Чехия. Она тоже образована шестигранными столбами из базальта.

Выходы базальта в Калифорнии

Курильские острова. Мыс Столбчатый.

Это уникальное геологическое образование в виде сплошного каменного выступа, поднимающегося на самом берегу моря высокой отвесной стеной. Излившиеся вулканические породы образовали узкие 4-х, 5-ти и 6-ти угольные столбы, так называемые столбчатые отдельности. У подножия столбчатой стены в беспорядке лежат, подобно отпиленных дровам, отшлифованные бруски. Выровненная морскими волнами прибрежная платформа создает иллюзию вымощенного паркета, а сохранившиеся от разрушения одиночные столбы похожи на остатки сломанного забора. Находится мыс на Курилах, остров Кунашир. Удивительно, что такую идеальную композицию создала случайность природы, невозможно поверить, что столбчатая структура образована стекавшими здесь когда-то давно потоками лавы, каждый столб имеет шестигранное сечение. Невообразимое сочетание красоты, величия и вдохновения.

Украина. Заказник «Базальтовые столбы»

Подобные шестигранные столбы имеются и в Украине. Это геологический заказник «Базальтовые столбы», который расположен около села Новый Берестовец Костопольского района Ровенской области.

Рис.7.1.Геологический заказник «Базальтовые столбы»

Базальтовые столбы в Украинском Полесье, имеют в поперечном перерезе, – форму от четырехгранных до семи- и даже восьмигранных. Толщина столбов колеблется в пределах от 0,6 до 1,2м. Преобладают с толщиной 0,8-1,0м. Высота – от 3-х до 30м.

Рис.7.3.Общая протяжность отслоений базальта в пределах заказника 180-230м.

Рис.7.4. Столбы имеют необычное свойство давать прямой ровный раскол. Поэтому при добыче их можно разделить на блоки длиною 1,5-3 метров.

Армения. Ущелье Гарни

Ущелье Гарни в Армении, которое находится в 23 км к востоку от Еревана, также славится тем, что здесь находятся такие же шестигранные столбы. Гигантские вертикальные базальтовые колонны создают впечатление связующих звеньев, которые соединяют небо и землю.

Происхождение шестигранных столбов

Как видно из перечисленных примеров, на Земле имеется не так мало мест, обладающие такими интересными геологическими особенностями. Поэтому образование столбов правильной шестигранной формы является процессом более закономерным, чем случайным. Покажем теперь, как объясняет этот геологический феномен официальная наука.

Ученые установили, что подобные колонны образуются, когда стремительно выброшенная вверх лава, медленно остывая, кристаллизуется и принимает вот такую своеобразную форму. Если говорить более подробно, то столбчатая отдельность является проявлением трехмерной сети трещин, которая образуется при остывании лавовых потоков, силлов, даек и других малоглубинных интрузий. Породы, по которым образуется столбчатая отдельность, могут быть произвольного состава, но чаще всего это базальты и долериты. При быстром остывании лавовых потоков или маломощных интрузий образуется ячеистая система напряжений, которая направлена перпендикулярно поверхности (или по максимальному температурному градиенту). В направлении этих напряжений затем развиваются линейные трещины, которые и образуют столбчатую отдельность. Иногда столбы сужаются к верхней части потока, образуя колоннаду. Возможно, это связано с различной скоростью остывания верхней и нижней частей потока.

Американские исследователи Горинг и Моррис из Торонто проверили эту гипотезу весьма оригинальным способом. А именно посредством крахмала, воды и паяльной лампы. Меняя режимы нагревания смеси крахмала с водой, ученые заставили засыхать его с разной скоростью. И в результате получили почти такие же колонны и плиты, что и в природе, только из кукурузного крахмала, и меньшего масштаба. Как пишут исследователи в своем отчете, чем медленней остывает смесь (в реальной жизни - лава), тем крупнее получаются плиты или столбы. Наряду с шестигранниками они получали и восьмигранники и другие структуры. То есть количество граней в них может меняться в зависимости от скорости остывания или высыхания. Авторы исследования (его детали можно найти в пресс-релизе университета Торонто) утверждают, что найденный ими коэффициент, связывающий скорость остывания (или высыхания) позволяет предсказывать размер ячеек и в других похожих процессах, вроде высыхания корки грязи или растрескивания слоя вечной мерзлоты.

Рис.9 Колонны (столбики), полученные посредством крахмала, воды и паяльной лампы. Меняя режимы нагревания смеси крахмала с водой, ученые заставили засыхать его с разной скоростью. И в результате получили почти такие же колонны и плиты, что и в природе, только из кукурузного крахмала, и меньшего масштаба

Итак, как мы видели, ученые установили, что колонны шестигранной формы появляются при остывании магмы, когда температурный градиент достигает определенной величины. Однако это совсем не объясняет, почему колоны в вертикально плоскости обладают формой правильного многогранника, почему остывающая магма лишь иногда создает такую удивительную форму колонн, тогда как в большинстве случаев интрузии имеют, как правило, неправильную форму, почему возникают колонны, а не кубики или призмы и т.д. Чтобы понять, как происходит образование столь удивительного природного феномена, обратимся к экспериментальным данным, которые устанавливают причины возникновения порядка из хаоса.

2. Порядок из хаоса

Образование шестигранных колонн, которые мы рассмотрели выше, является типичным примером образования порядка из хаоса, поскольку чаще всего магма изливается в виде хаотичных потоков, которые сплошь и рядом покрывают землю. Самопроизвольное проявление внутри застывающей магмы фигур правильной формы хоть и появляется на планете, но является все-таки очень редким явлением. Вообще, надо сказать, самопроизвольные процессы для ученых представляют собой одну из любопытнейших тайн природы. Поэтому современная наука целенаправленно изучает природные процессы, которые происходят сами по себе. Однако, как правило, самопроизвольно происходят только те процессы, которые идут с разрушением структуры, т.е. распад атомного ядра, расщепление сложных молекул на простые и т.д. Именно такие процессы явления являются самопроизвольными и необратимыми.

Другим примером подобных процессов является остывание горячих тел, тогда как нагревание их самопроизвольно происходить не может; прыгающий мяч, в конце концов, останавливается, однако покоящийся мяч самопроизвольно не начнет подскакивать. Природа необратимых явлений, которые самопроизвольно могут протекать только в одну сторону и никогда в другую, также до сих пор остается загадочной. Поэтому, когда обнаружились процессы, которые могут самопроизвольно создавать упорядоченные структуры, то это, естественно, не могло остаться без внимания.

Впервые на такие явления обратил внимание создатель новой, неравновесной термодинамики И. Пригожин. Он изучал процессы по самоорганизации вещества в разнообразных хаотичных системах. Причем появление такой спонтанной самоорганизации Пригожин объяснял, прежде всего, флуктуациями в неравновесных незамкнутых системах, где флуктуацией, по его определению, является случайное отклонения некой величины, характеризующей систему из большого числа единиц, от ее среднего значения (см. книгу И.Пригожина «Самоорганизация в неравновесных системах. От диссипативных структур к упорядочению через флуктуации»). Работы И. Пригожина по теории необратимых процессов в открытых неравновесных системах были удостоены Нобелевской премии по химии за 1977 год.

Ячейки Бенара

Обратимся к такому интересному физическому явлению, как ячейки Бенара, образующиеся в жидких средах. С этих ячеек начинал изучать процессы самоорганизации Пригожин. Ячейками Бенара называются конвективные ячейки, образующиеся в слое подогреваемого масла. Если мы будем постепенно нагревать снизу не слишком толстый слой вязкой жидкости, то до определенного момента отвод тепла от нижнего слоя жидкости к верхнему обеспечивается одной лишь теплопроводностью, без конвекции. Однако когда разница температур нижнего и верхнего слоев достигает некоторого порогового значения, система выходит из равновесия и происходит поразительная вещь. В нашей жидкости возникает конвекция, при которой ансамбли из миллионов молекул внезапно, как по команде, приходят в согласованное движение, образуя конвективные ячейки в форме правильных шестиугольников.

Рис.11. Эксперимент с силиконовым маслом, разлитым на плоской горячей поверхности, демонстрирует строго регулярную пространственную структуру с периодичностью, кратной толщине жидкого слоя. На фотографии видны выходящие из центра и сходящиеся по сторонам шестигранника конвективные потоки масла. На границах соприкасающихся сторон в местах стекания сформированы затененные каналы, свидетельствующие о том, что боковая поверхность тороида криволинейная и не имеет скачкообразных переходов.

Удивительные шестигранные ячейки появлялись на поверхности масла в тот момент, когда разница температур между верхним и нижним слоем достигала определенной величины. Впервые такую картину наблюдал Бенар, поэтому явление получило название ячейки Бенара.

С физической точки зрения, когда в жидкости возникает конвекция, при которой ансамбли из миллионов молекул внезапно приходят в согласованное движение, образуя конвективные ячейки в форме правильных шестиугольников, означает, что большинство молекул начинают двигаться с почти одинаковыми скоростями. Однако такое поведение молекул противоречит и положениям молекулярно-кинетической теории, и принципу порядка Больцмана из классической термодинамики. Почему же беспорядочное движение молекул резко изменило свою хаотичную природу? И.Пригожин рассматривал неустойчивость Бенара, как яркий пример спонтанной самоорганизации структур, или образование порядка из хаоса. Он характеризует возникшую ситуацию как флуктуацию, стабилизируемую путем обмена энергией с внешним миром. Причем Пригожин предполагает, что, если в классической термодинамике тепловой поток считается источником потерь (диссипации), то в ячейках Бенара он становится источником порядка.

Пригожин считал, что система, удаляясь от состояния равновесия (т.е. от состояния с равномерной температурой по всему объему жидкости), в итоге достигает критической точки неустойчивости (точки бифуркации), в которой возникает упорядоченный паттерн. Неравновесное состояние, поддерживаемое непрерывным потоком тепла через систему, генерирует сложный пространственный паттерн, в котором миллионы молекул движутся согласованно, формируя шестиугольные конвекционные ячейки.

Турбулентность в виде ячеек Бенара часто встречается в природе. Высохшие озера, солончаки и другие явления являются результатами конвективных процессов, сопровождающих высыхание приповерхностных зон. Также, например, поток теплого воздуха, идущий от поверхности земли вверх, может образовывать завихрения в виде шестиугольников, которые оставляют свои отпечатки на песчаных барханах в пустыне и в снежных полях Арктики.

Химическая реакция Белоусова-Жаботинского

Другой впечатляющий пример самоорганизации, который был подробно изучен Пригожиным и его коллегами в Брюсселе, называется «химические часы». Это химические реакции, в которых наблюдаются поразительные автоколебания. Впервые такую химическую реакцию наблюдал в 1951 году советский химик Борис Белоусов, изучая окисление лимонной кислоты броматом калия в кислотной среде в присутствии ионов церия. Он обнаружил у этой химической системы автоколебания, при котором менялся цвет раствора от бесцветного к желтому и обратно. Дальнейшее развитие исследований этой реакции проводил А.Жаботинский. Он исследовал механизм реакции и предложил первое объяснение ее механизма, а также простую математическую модель, которая была способна демонстрировать колебательное поведение.

Рис.12.1. Изменение цвета реакционной смеси в реакции Белоусова – Жаботинского с ферроином

Посмотрим на физическую сторону этого процесса. В реакционной смеси в реакции Белоусова – Жаботинского с ферроином участвует два типа молекул, «красные» и «синие». Движение молекул хаотично, поэтому в любой из частей сосуда концентрация «синих» и «красных» молекул будет несколько отклоняться от средней то в одну, то в другую сторону, а общий цвет реакционной смеси должен быть фиолетовым с бесконечными переходами в сторону синего и красного. А вот в химических часах мы увидим нечто совершенно иное: цвет всей реакционной смеси будет чисто-синий, затем он резко изменится на чисто-красный, потом опять на синий и т.д. Если в ячейках Бенара речь шла о согласованных механических движениях молекул, то здесь мы имеем дело со столь же согласованными, «как по команде», их химическими превращениями, создающими, так называемые, химические часы.

Как отмечает Пригожин, «столь высокая упорядоченность, основанная на согласованном поведении миллиардов молекул, кажется неправдоподобной, и если бы химические часы нельзя было наблюдать „во плоти“, вряд ли кто-нибудь поверил бы, что такой процесс возможен». Действительно, сообщение Белоусова об открытии автоколебаний в химических системах было встречено в научных кругах скептически. Статью Белоусова дважды отклоняли в редакциях советских журналов, поэтому опубликовать результаты исследований колебательной реакции он смог только лишь спустя 8 лет, и только в сокращённом виде.

Рис.12.2. В 1969 году Жаботинский с коллегами обнаружили, что если реагирующую смесь разместить тонким плоским слоем, в нём возникают волны изменения концентрации, которые видны невооружённым глазом в присутствии индикаторов.

Рис.12.3. Химические волны в реакции Белоусова-Жаботинского

Смотреть реакцию Белоусова-Жаботинского на Youtube

Фигуры Хладни

Не смотря на то, что Пригожин не рассматривал этого явления, поскольку в его основе лежит колебательное движение, тем не менее, я отношу его также к процессам самоорганизации, считая, что фигуры Хладни являются одним из ярчайших примеров образования порядка из хаоса. Ведь Пригожин изучал только те явления, когда автоколебания порождались явно не колебательными процессами. Хотя в дальнейшем мы покажем, что это не так.

Фигуры Хладни или удивительные узоры впервые были полученные немецким ученым Эрнстом Хладни (1756-1827) при помощи звука на обыкновенном песке. Насыпав на плоскую тонкую пластину песок, Хладни проводил смычком по одному из краев пластины. Песок, хаотично разбросанный первоначально по пластине, начинал смещаться и выстраивать красивые геометрические узоры. В зависимости от того, в каких местах пластина была закреплена, и на каком участке проводили смычком, картина геометрических узоров из песка существенно менялась.

Вид их зависел как от формы пластинки, так и от места ее закрепления, а также и от тех мест, в которых проводили смычком и прикасались пальцем (для задержания колебания и образования узла). Кроме того, влияние оказывала и степень нажатия смычка и скорость его движения. На квадратных пластинках наиболее простые фигуры получаются в виде креста, расположенного или параллельно сторонам или по диагоналям.

На круглых пластинках получаются вообще звездообразные фигуры. Каждой фигуре соответствует определенный тон; притом, чем сложнее фигура, тем тон выше.

Рис.13.2. Песок сбрасывается с тех мест, где происходит усиление амплитуды и собирается на узловых линиях. Такие фигуры показывают картину узловых линий, рассекающих поверхность пластинки при ее колебаниях. Вид фигур зависит от формы пластинки (круглая или квадратная), положения закрепленных точек, а также от того, в каком месте проводить смычком.

Объяснить образование порядка из хаоса в этом случае не сложно. Всему виной являются звуковые волны. Под действием смычка пластина начинает вибрировать, т.к. в ней распространяются звуковые волны. Поскольку пластина ограничена в пространстве в ней могут укладываться определенное число волн, которые кратны длине и ширине пластины. При определенных колебаниях в пластине возникают стоячие волны. Образование стоячих волн относится к процессу интерференции (сложения волн). При интерференции волны от разных источников складываются, образуя причудливую картину. Если частоты колебаний являются кратными между собой, то получаемая картина при этом остается неподвижной, «стоячей».

Несколько слов скажу о стоячих волнах, и что они собой представляют. Чаще всего стоячие волны можно наблюдать на длинном шнуре. Если один конец шнура колеблется с различной частотой, то на шнуре возникает разное количество полуволн. Интересными особенностями стоячих волн являются, так называемые, узлы и пучности. На картинке 5 можно видеть, как образуются стоячие волны на длинном шнуре.

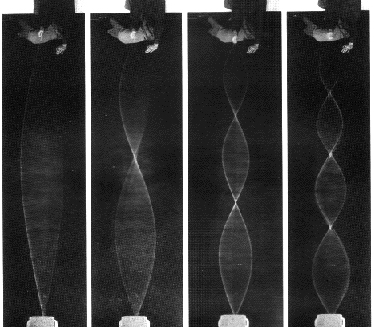
Рис.13.3. На шнуре образуются чередующиеся неподвижные точки и точки, в которых размах колебаний наибольший. Неподвижные точки называются узлами стоячей волны, а места наибольшей амплитуды колебаний – ее пучностями. Расстояние между двумя соседними узлами (или двумя соседними пучностями) равно половине длины шнура. Чем быстрее мы колеблем нижний конец шнура, т. е. чем выше частота, тем короче длина волны и тем больше узлов и пучностей укладывается на шнуре.

Стоячие волны никуда не двигаются, они как бы все время находятся на одном месте. Причем волновая картина сохраняется неизменной в течение длительного времени. Одной из разновидностей стоячих волн является голограмма, которая тоже образуются благодаря стоячим волнам, правда, здесь уже используются световые волны. В принципе, образование стоячих волн – это и есть результат интерференции, в нашем случае для длинного шнура, например, складываются падающая волна и отраженная волна.

Такие же стоячие волны образуются и на пластинах в эксперименте Хладни. Как видно из рисунка песок сбрасывается с тех мест, где колебания пластины максимально, и собирается на узловых линиях, т.е. в местах, где колебаний нет совсем. Фактически фигуры Хладни показывают картину узловых линий, рассекающих поверхность пластинки при ее колебаниях. Вид фигур зависит от формы пластинки (круглая или квадратная), положения закрепленных точек, а также от того, в каком месте проводить смычком. Изучение этого явления оказало существенное влияние на развитие науки, а Хладни в истории науки остался как основоположник экспериментальной акустики.

Эксперименты Йенни

Несколько позже доктор Ханс Йенни усовершенствовал эксперимент Хладни. Он наблюдал интерференцию не только на плоскости, но и в объемном варианте. Для проведения своих экспериментов Йенни создал специальный аппарат, который назвал тоноскоп. Он получал геометрию звуковых колебаний, используя тонкие контейнеры, наполненных различными средами: песком, мокрым гипсом и разными типами жидкостей, состоящих из тонкодисперсных сред. Находясь в состоянии покоя, взвесь мельчайших частиц равномерно распределялась по всему объему жидкости, и вода становилась мутной. Когда контейнер приводили в колебательное движение с различной частотой и амплитудой, частицы в жидкости складывались в упорядоченные и хорошо видимые геометрические узоры, обладающие двумерной и трехмерной структурой (рис.). На рис. представлена интерференция волн, которую Йенни получал в вибрирующей капельке воды, содержащей мелкие частицы взвеси. Эти частицы формировали трёхмерные звезды, двойные четырёхгранники в кругах и много других фигур. Чем выше была частота колебаний, тем сложнее получались фигуры.

Рис.14.1. Интерференция волн в вибрирующей капельке воды

Суть эксперимента понять не сложно. Колебания на пластине или внутри пространства создают волны, которые, интерферируя между собой, создают устойчивые волновые картины. Глядя на получающиеся картины, мы видим, что частицы скапливаются в тех местах, где отсутствует какая-либо вибрация. Такие области образуются за счет гашения колебаний и соответствуют минимальным значениям энергии. И наоборот, области пространства, в которых происходит усиление амплитуды в результате сложения колебаний, свободны от частиц. Поскольку само пространство как бы выталкивает их из этих мест. Поэтому, благодаря мельчайшим частицам, мы можем наблюдать сложную картину интерференции, создаваемую колебательными процессами.

Таким образом, получаем, что интерференционные минимумы, где скапливаются мелкие частицы, являются энергетически более выгодными. Поэтому частицы стремятся занять область с минимальной потенциальной энергией. В местах интерференционных максимумов появляются как бы потенциальные барьеры, которые не позволяют частицам свободно перемещаться в пространстве. При отсутствии колебаний мелкие частицы могли свободно диффундировать по всему пространству, равномерно заполняя весь объем. Но интерференционные максимумы создают «непреодолимый» барьер для диффундирующих частиц, поэтому они скапливаются только в местах интерференционных минимумов.

Современные исследования полей вибрации еще более усложнили эксперименты. Вместо крупных твердых частиц теперь используются всевозможные взвеси тонкодисперсных веществ, струйки пара или дыма и др. Но чтобы не использовали исследователи, для того чтобы увидеть энергетическую картину, составляющую поле вибрации, результат оставался неизменным. Каждый раз получались изумительные узоры, представляющие собой энергетическую структуру вибрационных полей (см. рис.14.2).

Рис.14.2. Интерференционная картина звуковых волн, полученная экспериментатором Фуллером на воздушном пузырьке, помещенным в чернила, сайт http://www.cymatics.org/

Российский экспериментатор Кушелев усовершенствовали способ наглядного представления фигур Хладни в виде электромагнитного аналога. Здесь фигуры Хладни образуются на поверхности электромагнитного резонатора, чувствительной к одному из электромагнитных параметров. Например, если резонатором является алюминиевая фольга, то чувствительными элементами могут быть элементы пенопластовой подложки. Когда через фольгу пропускали ток, в местах пучности электрический ток был максимальным. Ток настолько сильно нагревал фольгу, что пенопластовая подложка под ней плавилась. Однако в узлах стоячей электромагнитной волны сила тока была нулевой, поэтому плавления подложки на ней не происходило. В результате получилась рельефная фигура подобная фигурам Хладни.

Кушелев также сумел получить виртуальные фигуры Хладни при помощи компьютерной программы HFSS, которая позволяет получать такие фигуры виртуально, рассчитывая узлы и пучности электромагнитного поля на поверхности и в объеме резонатора. Причем с помощью программы HFSS можно получать не только двухмерные, но и трёхмерные фигуры Хладни.

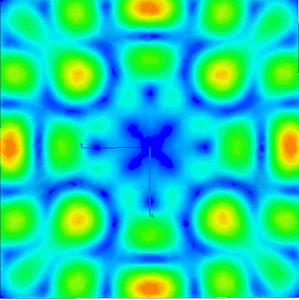
Рис.14. Кушелев получает виртуальные фигуры Хладни при помощи компьютерной программы HFSS

Подведем небольшие выводы по фигурам Хладни. Во-первых, эти фигуры дают нам возможность видеть, какое влияние на материю оказывают стоячие волны (или интерференция волн) различной природы (звуковые, электромагнитные). Во-вторых, дают возможность визуализировать интерференционные картины, создаваемые невидимыми волнами. Ведь сами звуковые волны или электромагнитные волны мы видеть не можем, а вот результат их влияния на вещество наблюдать можно. В-третьих, позволяют экспериментально изучать такое интересное явление, как интерференция.

Мы подошли к еще одному загадочному природному явлению – снежинкам. Хотя, казалось бы, что может быть проще знакомых всем с детства снежинок. Многие, наверно, не раз любовались причудливыми узорами, образуемыми ими. А ведь это тоже образование порядка из хаоса. Однако трудно представить, как могут хаотично двигающиеся в воздухе молекулы водяного пара вдруг начать спонтанно образовывать геометрически правильные и изящные снежинки.

Когда при температурах ниже нуля водяной пар переходит в твердое состояние, то вместо капель воды образуются ледяные кристаллы. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них – новые, и так получаются разнообразные формы звездочек – снежинок. Однако, не смотря на то, что наука уже довольно много узнала, как и где образуются снежинки, тем не менее, до сих пор не понятно, почему на всех лучах снежинки, как правило, повторяется один и тот же узор? Откуда молекула одного луча «знает» куда ей прикрепиться, чтобы соблюсти тот же узор, что и на других лучах?

С точки зрения современной науки снежные кристаллы образуются в холодных облаках высоко над землей. На очень больших высотах, где температура доходит до 40-50 градусов мороза, водяной пар в облаках замерзает, формируясь в кристаллики льда. В облаках, расположенных ниже, пар замерзает медленнее, обычно предварительно пристав к какой-нибудь взвешенной в воздухе частице. При исследовании множества снежинок под микроскопом обнаружено, что около 3/4 снежинок содержат в центре мельчайшие частицы глины. По мнению ученых, снежные кристаллы по форме бывают четырех типов. Простейшая форма - длинные игольчатые кристаллы. Все остальные типы имеют шесть сторон, то есть они обладают гексагональной (шестиугольной) формой.

Научно установлено, что основная форма снежинки зависит от температуры, при которой она образуется. Причем понятно, чем выше облако, тем оно холоднее. Высокие перистые облака, образующиеся на высоте 10км и находящиеся при температурах 35-40 градусов мороза, состоят из кристалликов-призм, которые выглядят, как блестящие подвески люстр, сверкающие в лучах солнца. Если температура в облаке в пределах 0-3 градусов мороза, то образуются плоские шестиугольники, при 3-5 градусов мороза формируются игольчатые кристаллы, при 5-8 градусов мороза образуются столбики - призмы, при 8-12 градусов мороза вновь появляются плоские шестиугольники, при 12-16 градусов мороза возникают первые звездчатые снежинки. При дальнейшем снижении температуры образуются снежинки всех типов.

Рис.15.1. Фотографии снежинок из атласа Бентли и Хамфри (по кн. А.В.Шубникова и В.А.Копцик «Симметрия в науке и искусстве» М., «Наука», 1972 г.).

Посмотрим, как можно объяснить образование снежинок с точки зрения голографической модели, в которой «виной» всему являются волновые процессы, а также образование стоячих волн или, другими словами, явление интерференции. Первое, что сразу бросается в глаза, это одинаковость в образовании фигур Хладни и снежинок. Поэтому вполне можно допустить, что молекулы водяного пара скапливаются вдоль узловых линий точно так же, как песок скапливается в узловых линиях на пластине, образуя фигуры Хладни. Но это возможно только в том случае, если у нас имеются стоячие волны с их характерными образованиями в виде узлов и пучностей.

Но откуда в облаке могут образоваться стоячие волны? Да очень просто! Если мы вспомним, как образуются ячейки Бенара, то не сложно представить, что и в облаках могут возникнуть конвективные потоки воздуха, совсем как на поверхности масла в тот момент, когда разница температур между верхним и нижним слоем достигает определенной величины. Удивительные шестигранные ячейки также появляются и в облаке, когда разница температур между двумя слоями воздуха достигает определенной величины. То, что в облаке вполне могут существовать конвективные потоки доказать не трудно, достаточно посмотреть на кучевые облака. Их явно кудрявая форма вызвана как раз тем, что температурный градиент между слоями воздуха образует характерную конвекцию, почти как в ячейках Бенара. Хотя ячейки и получаются не совсем правильной формы, но природа явления одна и та же. Особенно интересны в этом плане так называемые вымяобразные облака. Когда смотришь на такие облака, то они удивительно напоминаю ячейки Бенара, разве что из-за ветра они обладают не столь правильной формой как в нагреваемом масле.

Рис. 15.3. Вымяобразные облака похожи на ячейки Бенара, хотя они из-за потоков воздуха обладают не столь правильной формой как ячейки в нагреваемом масле.

Когда на высоте примерно 10 км над землей между двумя тоненькими (или даже тонюсенькими) слоями воздуха появляется нужный температурный градиент, воздух приходит в конвективное движение, образуя ячейки подобно Бенаровским. Фактически, каждая такая ячейка представляет собой прообраз будущей снежинки.

Но это еще не все. Дальше в этих ячейках еще дополнительно возникают стоячие волны. Теперь мы могли бы увидеть фигуры Хладни в ячейках Бенара, если бы, конечно, знали, как это сделать. С появлением стоячих волн в ячейках Бенара, движение молекул воздуха от конвективного переходит к колебательному, и молекулы пара постепенно смещаются к линиям узлов, так же как песок на пластине в экспериментах Хладни. Вдоль узловых линий молекулы пара уже не колеблются, поэтому могут смерзаться, образуя цельную ледяную конструкцию в виде снежинки.

Несколько слов можно добавить по поводу природы стоячих волн в бенаровских ячейках. Согласно голографической модели голограмма молекул водяного пара имеет вид, как на рис. Не сложно понять, что она и задает тот самый волновой паттерн, в котором образуются стоячие волны, что в дальнейшем порождают снежинку.

Теперь становится понятно, почему на всех лучах снежинки повторяется один и тот же узор и откуда каждая молекула «знает» куда ей прикрепиться, чтобы соблюсти ту же геометрию, что и на других лучах. Ведь все молекулы водяного пара скапливаются вдоль узловых линий точно так же, как песок скапливается в узловых линиях на пластине, образуя фигуры Хладни.

Еще обратим внимание на то, что в фигурах Хладни на узор оказывает изменение как форма пластины, так место ее закрепления. Оказывает влияние и место, в котором проводят смычком или прикасаются пальцем (для задержания колебания и образования узла), также влияние оказывает и степень нажатия смычка, и скорость его движения. Как видно, факторов, которые сказываются на получаемых изображениях, оказывается слишком много. Отсюда следует, что невозможно получить двух одинаковых снежинок, так как здесь точно также сказываются малейшие изменения как в форме ячейки, так и образовании стоячих волн внутри нее, где единственным неизменным элементов остается только шестигранность.

Круги на полях

Следующим примером образования порядка из хаоса будут круги на полях. Это тоже интересное явление, которое давно будоражит человеческие умы. Тем более, что официальная наука старательно делает вид, что не замечает этого феномена. Но, тем не менее, такое явление природы существует. Это явление, при котором на возделываемых полях в одночасье возникают рисунки в виде колец, кругов и других геометрических фигур, образованные полегшими растениями. Такие рисунки могут быть небольшими или иметь настолько большой размер, что целиком их можно видеть лишь с самолёта.

Вначале, когда на полях образовывались простые круги, «научные круги» строго придерживались мнения, что это шутки местных злоумышленников. Но когда стали появляться сложные круги в виде различных пиктограмм удивительно правильных геометрических форм, то стало очевидно, что человеческим рукам это сделать не под силу даже при современно технике. И тогда осталось уповать только на инопланетян, которые явно из благих побуждений оставляют нам разные послания вот в такой форме, как круги на полях. Ибо иных способов общаться с нами у бедных инопланетян нет…

Круги на полях – это очень красивые образования. Обычно они образуются ночью в течение нескольких секунд между 23:30 и 4:00 часами. Если проанализировать фотографии кругов разных лет, то легко прослеживается тенденция к усложнению узора «круга». Круги давно уже не круги. Это уже сложные комплексные образования из квадратов, линий, эллипсов, ромбов. При построении фигур используются чрезвычайно сложные формы Евклидовой геометрии. Поэтому все чаще вместо кругов говорят о фигурах или пиктограммах.

Рис.16.1 Круги на полях в виде сложной пиктограммы появились 07.07.1996 года недалеко от Стоунхенджа (Великобритания)

Рис.16.3.«Дно» фигуры может иметь несколько ровно уложенных слоев, иногда наблюдается до пяти таких слоев, и пшеница в каждом слое закручена в сторону, противоположную предыдущему. Каждый колосок в них лежит аккуратно рядом с другим.

Рис.16.4.В центре круга колосья могут хитрым образом переплестись, и в центре часто может находиться лишь один прямостоящий колос, или нетронутый пучок колосьев

Рис.16.5.В настоящих фигурах колосья не сломаны, а лишь изогнуты примерно в дюйме от земли, там, где находится первое коленце колоса

«Дно» фигуры может иметь несколько ровно уложенных слоев, иногда наблюдается до пяти таких слоев, и пшеница в каждом слое закручена в сторону, противоположную предыдущему. Каждый колосок в них лежит аккуратно рядом с другим. Но растение не погибает и продолжает расти. В настоящих фигурах колосья не сломаны, а лишь изогнуты примерно в дюйме от земли, там, где находится первое коленце колоса. Настоящие пиктограммы обычно выглядят идеальными, в них присутствует абсолютная точность выверенных линий. В отличие от настоящих кругов в подделках колосья просто свалены в разные стороны и потоптаны, и, конечно же, сломаны. Края настоящих фигур также сильно отличаются от фальшивок, так как выведены с хирургической точностью. Колосья закручены в спираль, в которой используются те же логарифмические пропорции, что и в числах Фибоначчи или золотой пропорции.

В центре круга колосья могут хитрым образом переплестись, и в центре часто может находиться лишь один прямостоящий колос, или нетронутый пучок колосьев. Причем все растения продолжают расти, хотя собрать урожай с полегших колосьев уже нельзя. И как сказано выше, о причине возникновения кругов на полях официальная наука пока не даёт никакого определённого ответа.

Объяснение этому феномену можно дать с точки зрения голографической модели. Возникновение кругов на полях такой правильной геометрической формы сродни возникновению порядка из хаоса. А точнее это результат влияния образующихся стоячих волн в интерференционной картине. В принципе этот процесс объясняется точно так же, как и образование фигур Хладни, поэтому особенно останавливаться на нем не будем. В пиктограммах так же, как в фигурах Хладни есть места, где амплитуды волн складываются, поэтому их влияние на биологические объекты усиливаются. В других местах, где происходит вычитание амплитуд, растения остаются не тронутыми. А в целом получается красивая геометрически правильная картина. В отличие от фигур Хладни, которые создаются звуковыми волнами, круги на полях «рисуются» волнами времени. О том, что представляют собой волны времени, скажем чуть позже.

3. Второе начало термодинамики

«Летай иль ползай, конец известен: все в землю лягут, все прахом будет…» (М.Горький)

Чем же примечательны рассмотренные нами примеры самоорганизации? Как сказано выше, современная наука целенаправленно изучает необратимые природные процессы, проходящие самопроизвольно. Например, само по себе происходит остывание горячих тел, но нагревание их самопроизвольно происходить не может; прыгающий мяч всегда останавливается, но покоящийся мяч сам по себе не начнет подпрыгивать. Самопроизвольно происходит разрушение вещества, например, распад атомного ядра, расщепление сложных молекул на простые и т.д., но синтез вещества требует неимоверно сложных процессов и сам по себе происходить не может. Как видно, в природе повсеместно происходят процессы по возрастанию разрухи и хаоса.

Понятно, что главную роль во всех этих процессах играет превращение энергии. Как мы знаем, энергия ниоткуда не берется и никуда не исчезает, она может только переходить из одного вида в другой (закон сохранения энергии). Но ученые давно обнаружили, что все виды энергии, в конечном счете, превращаются в тепловую энергию, которая в дальнейшем рассеивается в пространстве. Такую энергию назвали диссипативной. Это наблюдение легло в основу основного физического закона термодинамики, которое получило название второго начала. (Естественно, что первым началом термодинамики является закон сохранения энергии). Так вот, второе начало термодинамики устанавливает, что все процессы в природе самопроизвольно могут происходить только с увеличением хаоса и беспорядка. Хочу подчеркнуть, что закон только устанавливает этот факт, но никак не объясняет. В дальнейшем был введен термин – энтропия, который количественно характеризовал меру хаоса в системе. Поэтому второе начало стало звучать несколько иначе, а именно, все процессы самопроизвольно могут идти только в сторону увеличения энтропии, т.е. в сторону увеличения беспорядка и хаоса.

Когда Клазиус и Томсон (Кельвин) в 1865 году открыли закон, имеющий название второго начала термодинамики, то получили из него неожиданные выводы. Так как такой процесс рассеяния тепла (диссипация) необратим, то рано или поздно все звезды погаснут, все активные процессы в природе прекратятся, и наступит состояние, которое Клаузиус назвал "тепловой смертью" Вселенной.

Однако мы же видим, что никакой деградации не происходит, и природа повсеместно усложняется: создаются сложные многоэлектронные атомы, сложные молекулярные системы, организмы эволюционируют от простейших одноклеточных к многоклеточным организмам со все возрастающей сложной дифференциацией внутренних органов или подсистем и т.д. В чем состоит принципиальная разница между сложной структурой и простой? Ответ очевиден. Когда простые системы объединяются в сложную, им необходима энергия, которая соединяет подсистемы. Эта энергия является энергией связи. Так нуклоны в ядре объединены энергией связи, в процессах фотосинтеза энергия связи получается из световой энергии, за счет которой образуются сложные органические молекулы из простых веществ. Таким образом, во всех самоорганизующихся системах внешняя хаотичная энергия превращается в связанную энергию или энергию связи. Когда сложное вещество распадается на простые составляющие, эта энергия связи чаще всего выделяется в виде тепла.

Родоначальник новой термодинамики Пригожин полагает, что процессы самоорганизации систем тоже могут происходить произвольно, но только в результате случайных флуктуаций. И за их образование несет ответственность та самая диссипативная энергия, которая рассеивается в пространстве при превращении энергии в тепловую. Таким образом, И.Пригожин считает, что диссипативная энергия способна порождать сложные системы из простых. В этом случае второе начало термодинамики приобретает совершенно иной философский смысл, потому что энтропия оказалась тем самым «сырьем», из которого диссипативные структуры могут создать (а могут и не создать – это дело случая!) более высокую, чем прежде, упорядоченность.

Пригожин показал, для того, чтобы в некоторой системе начались процессы самоорганизации, она должна быть, как минимум выведена из стабильного, равновесного состояния. В ячейках Бенара неустойчивость имеет простое механическое происхождение. Нижний слой жидкости в результате нагрева становится все менее плотным, и центр тяжести смещается все дальше наверх; по достижении же критической точки система «опрокидывается» и возникает конвекция. В химических системах ситуация сложнее. Здесь стационарное состояние системы представляет собой ту стадию ее развития, когда прямая и обратная химические реакции взаимно уравновешиваются и изменения концентрации реагентов прекращаются. Вывести систему из этого состояния очень трудно, а в большинстве случаев – просто невозможно; не зря реакции типа «химических часов» были открыты лишь недавно, в 50-е годы минувшего века (хотя их существование было теоретически предсказано математиком Р. Вольтеррой еще в 1910 году).

Таким образом, упорядоченные структуры могут возникать только в открытых неравновесных системах. Это означает, что если система интенсивно обменивается энергией с окружающей средой, то в ней возникают условия для образования порядка из хаоса. Или другими словами, возникают такие типы структур, которые способны к самоорганизации, т.е. к переходу от беспорядка или «теплового хаоса», к упорядоченным состояниям. Пригожин назвал эти структуры диссипативными, стремясь подчеркнуть парадокс: процесс диссипации (т.е. безвозвратных потерь энергии) играет в их возникновении конструктивную роль. Еще раз подчеркну, что Пригожин считал, что замкнутых систем не существует, и все системы в той или иной мере обмениваются энергией с окружающей средой.

В отличие от него советский астрофизик Н.Козырев считал, что рассматривая системы в космическом масштабе, видно, что все они замкнуты. Вот, что он пишет по этому поводу в своей книге «Причинная механика…»: «Применяя физические законы для объяснения явлений звездного Мира, мы неизбежно распространяем на Вселенную и все следствия второго начала термодинамики. Во Вселенной же нет никаких признаков деградации, как вытекает из второго начала. Мир сверкает неисчерпаемым разнообразием, мы не находим в нем и следов приближения тепловой и радиоактивной смерти. По-видимому, здесь и заключается основное противоречие – противоречие очень глубокое, которое нельзя устранить ссылками на бесконечность Вселенной. Дело в том, что не только отдельные астрономические объекты, но даже целые системы в такой степени изолированы друг от друга, что их можно рассматривать как системы замкнутые. Для них тепловая смерть должна заметно приблизиться прежде, чем успеет прийти помощь со стороны. Такие деградированные состояния систем должны были быть преимущественными, а вместе с тем они почти незаметны. Оставаясь в рамках обычных законов механики и физики, остается считать, что наблюдаемая картина Мира является следствием или одной обширной, охватившей некогда весь Мир катастрофы, или следствием мелких, постоянно происходящих катастроф, обновляющих Мир».

Динамическая энергия

Толкование понятия "хаос" создателями неравновесной термодинамики существенно отличается от общепринятого понимания хаоса как максимума энтропии. У Пригожина хаос больше ассоциируется с понятием случайности, с хаотическим разнообразием флуктуаций в сложной системе, хаотическими отклонениями каких-то параметров от нормы. В основе такого хаоса лежит активное начало, причем в определенных условиях даже единичное отклонение, малое воздействие какого-то параметра может стать существенным для макропроцесса, и тогда может развиться новая организация.

Одним из главных достижений Пригожина является то, что он показал существование неравновесных термодинамических систем, которые, при определённых условиях, поглощая вещество и энергию из окружающего пространства, могут совершать качественный скачок к усложнению (диссипативные структуры). Причём такой скачок не может быть предсказан, исходя из классических законов статистики.

При всей своей прогрессивности выводы Пригожина явно имеют существенный недостаток, который состоит в том, что в его мире, или его термодинамике всем правит Его Величество Случай! А ведь мы в большей степени видим закономерные явления во всей эволюции мира, как во всей Вселенной, Галактике, так и на нашей планете. И это далеко не случайный процесс. Природа неуклонно постоянно движется от простого к сложному. Эта поступь прогрессивной эволюции еще не сбоила ни на одном из этапов. А если положить, что всем управляют случайные процессы, и жизнь зародилась тоже случайным образом, то на Земле никогда бы не было таких сложных организмов, какие мы наблюдаем. Более того, не было бы и нас с вами. Не зря же существует мнение, что вероятность появления жизни в первобытном океане настолько мала, что скорее ураган, пронесшийся сквозь гигантскую помойку, случайно соберет «Боинг-747».

Это означает, что эволюция не может управляться случайными процессами. Отдельные случайные процессы имеют место быть, но они не играют определяющей роли в природе. Эволюция мира – это закономерный процесс. Исходя из этого можно сделать основополагающий вывод: для того чтобы эволюция происходила на всех уровнях мироздания, нужны созидающие силы. И они в природе есть.

Теперь мы опять пришли к идее того, что должны существовать структурообразующие силы. И как мы знаем, роль таких созидающих сил играет время. Об этом уже говорилось неоднократно. Физическая природа времени и его созидающая роль описывается в книге «Что такое время?»

В отличие от диссипативной энергии, которую рассматривает Пригожин, нам приходится ввести новое понятие динамической энергии, которую несет в себе сущность времени. Поэтому у нас диссипативная энергия – это энергия хаоса, которая способна только разрушать сложные структуры, а вот динамическая энергия, которая суть время, это созидающая энергия. Именно она ответственна за создание сложных структур из простых.

И вот теперь мы избавились от парадокса, который существовал в термодинамике Пригожина, когда разрушающая энергия диссипации способна создавать сложные структуры. Для создания принципиально нового существует динамическая энергия, которая в виде времени втекает во все самоорганизующиеся системы. Она же затем в виде энергии связи остается внутри системы. Диссипативная энергия наоборот, разрушает сложные системы, преобразуя их в простые, путем разрушения внутренних связей подсистем. Причем как тот, так и другой процесс не являются случайными, т.к. здесь происходит закономерное преобразование одного вида энергии в другой.

Структурообразующая роль времени

Впервые на организующие свойства времени обратил внимание Н.Козырев в середине ХХ века. Он экспериментально обнаружил, что необратимые процессы, происходящие внутри системы, способны изменять энтропию процессов, происходящих снаружи, за счет изменения плотности времени в окружающем пространстве. При возрастании энтропии внутренней системы плотность времени в окружающем пространстве этой системы увеличивается, и наоборот. Фактически, проводя эксперименты с гироскопами, маятниками и крутильными весами, способными регистрировать направление хода времени, Козырев нашел способ определять возрастание или убывание энтропии, в виде изменения внутренней организованности системы. Многочисленные эксперименты, которые он проводил по измерению хода времени, показали, что время, втекая в систему, привносит в нее упорядоченность. Вытекающее из системы время уносит с собой организованность в виде диссипативной энергии, которая излучается при необратимых процессах.

Вот как пишет сам Козырев об этих экспериментах: «Плотность времени представляет собой некоторую скалярную величину, которая и наблюдалась в предыдущих опытах. Плотность времени убывает с расстоянием от создающего ее процесса. Поэтому должно наблюдаться и векторное свойство, соответствующее градиенту плотности, которое можно трактовать как излучение времени. Для обнаружения этого свойства было совершенно естественным обратится к крутильным весам. После многочисленных проб была найдена простейшая их конструкция, решающая поставленную задачу.

Произведенные с этими весами опыты показали, что стрелка весов, т.е. длинный конец коромысла, отталкивается от всех процессов, излучающих время, и притягивается к процессам, его поглощающим. Исследования показали, что стрелку весов притягивают очень многие процессы: любые процессы деформации тел, удары воздушной струи о препятствия, работа песочных часов, поглощение света, присутствие наблюдателя, все процессы, связанные с трением. Нулевой отчёт, т.е. нормальное положение стрелки устанавливается не кручением нити, а действием совокупности происходящих вокруг процессов. Наблюдавшиеся повороты весов происходили на десятки градусов, что соответствовало силам 10^-3 - 10^-4 дин. Таким образом, при весе коромысла в несколько граммов его повороты были вызваны составляющими 10^-6 - 10^-7 от действующих в системе сил» (Козырев H.А., "Астрономические наблюдения…»).

Хочу обратить внимание на слова Козырева, что нулевой отчёт, или нормальное положение стрелки устанавливается не кручением нити, а действием совокупности происходящих вокруг процессов. Это означает, что вокруг нас с вами существует множество систем, которые излучают или поглощают время (или ход времени по Козыреву). И стрелка крутильных весов устанавливается в равновесном состоянии только тогда, когда суммарная составляющая всех волн времени, действующих на стрелку, будет равна силе упругости закрученной нити.

Надо добавить, что любая система излучает и поглощает волны времени одновременно на всех этапах своего развития. Только, когда система молодая, интенсивность потока времени, которая втекает в систему, очень высока, поэтому система не только поглощает динамическую энергию, но и излучает ее во вне. Причем поток излучаемой на этом этапе динамической энергии много больше потока диссипативной энергии. Как говорят, молодость так и «брызжет» энергией. Со временем интенсивность потока динамической энергии падает и уже излучение диссипативной энергии становится преобладающим. Именно эти процессы наблюдал в своих экспериментах Козырев. Он говорил, что стрелка весов, т.е. длинный конец коромысла, отталкивается от всех процессов, излучающих время. Это как раз тот случай, когда излучение диссипативной энергии больше, чем излучение динамической энергии. Стрелка весов как бы выталкивается разрушительными силами, которые несет в себе диссипация. Но зато стрелка втягивается в те области, где имеется поток динамической энергии. И это выглядит, как поглощение времени системами, т.е. стрелка притягивается к процессам, которые активно поглощают динамическую энергию.

В нашей голографической модели структурообразующая функция времени играет определяющую роль. В книге «Что такое время?» показано, что время входит (втекает) в систему в виде волн. Но понятие «волны времени» не является физически корректным, поэтому более правильным будет использование термина хронооболочка. Этот термин заменяет нам представление о волнах времени, которые следуют из будущего в прошлое, проходя через настоящее. Но и хронооболочки, фактически, представляют собой стоячие волны. За счет различных квантовых состояний мы можем рассматривать хронооболочки и как стоячую волну, и как материальное тело. Как стоячая волна хронооболочка обладает внутренними колебательными процессами со своей частотой и амплитудой, которые зависят от размера хронооболочки и скорости поступающей энергии.

Хронооболочки могут дробиться (квантоваться) на более мелкие. Внутри одних хронооболочек появляются другие, и их колебательные процессы гармонично связаны между собой, т.к. устойчивость всей системы регулируется образованием взаимных субгармоник. Сама отличительная особенность гармоник заключается в том, что когда они образуют устойчивые стоячие волны, то в рамках одной волны должно укладываться целое число полуволн. Такую систему хронооболочек можно представить в виде колебательной системы. Организация мира складывается именно за счет колебательных (или волновых) процессов. Процессы образования сложных структур за счет колебательных процессов мы уже рассматривали на физическом явлении, известном, как фигуры Хладни.

4. Объяснение процессов самоорганизации

Покажем теперь, что в основе всех процессов самоорганизации лежат колебательные или волновые процессы. Причем следует сказать, что колебательные процессы не возникают сами по себе, они появляются на основе других колебательных процессов. Можно сказать, что одни колебания порождают другие колебания. Это является основным принципом причинно-следственных связей. Если в явлениях образования ячеек Бенара первичные колебательные процессы не столь очевидны, но, тем не менее, появление самих шестигранных ячеек определенно представляют собой стоячие волны на поверхности масла. А в реакции Белоусова колебательные процессы проявляются в чередовании химических реагентов.

Пригожин полагал, что волновые процессы, возникающие в системах, и есть то самое свойство, что отделяет упорядоченное поведение систем от хаотичного. Однако в любых системах самоорганизация возникает за счет волн времени, втекающих в нее с определенной скоростью. Но поскольку волны времени не несут импульса, как установил Козырев, то оказать влияние на материальные тела они не могут, какими бы маленькими они не были, например, молекулы, атомы. Но, тем не менее, когда температурный градиент в нагреваемом масле становится когерентен волнам времени, возникает явление резонанса, и появляются реальные стоячие волны на поверхности масла, образующие конвективные ячейки Бенара.

Другими словами, это означает, что поток тепла или скорость поступления энергии в систему сравнялся со скоростью втекания волн времени. При наступлении резонанса даже мельчайшее воздействие на систему приводит ее к упорядоченному состоянию. В химической реакции Белоусова – Жаботинского также упорядочивающую роль играют волны времени, и колебательные процессы в реакции возникают, когда наступает резонанс. Здесь стационарное состояние системы представляет собой ту стадию ее развития, когда прямая и обратная химические реакции взаимно уравновешиваются и изменения концентрации реагентов прекращаются. Поток энергии от одной части реагентов к другой в этот момент становится когерентен волнам времени (хронооболочке). Он усиливается и достигает максимума для красных молекул на первой «полуволне» хронооболочки, а на второй «полуволне» хронооболочки достигает максимума для синих молекул. Затем все повторяется сначала, и возникают «химические часы», которые «тикают» в соответствии с скоростью втекания волн времени в систему.

Таким образом, волновые процессы в ячейках Бенара и химической реакции Белоусова – Жаботинского, которые Пригожин определял, как возникновение упорядоченных структур из хаоса, на самом деле возникают за счет волн времени, поступающих в систему в виде потока энергии. Мы не видим волны времени, но мы видим результат их воздействия на вещество (молекулы масла или молекулы химических реагентов). Точно так же мы не видели звуковых волн в образовании фигур Хладни. Но видели результат их влияния на вещество (песок). Мы не видим волн времени, образующих круги на полях, но видим их воздействие на биологические системы на молекулярном уровне.

Теперь осталось пояснить, как образуются шестигранные колонны, о которых говорилось в первой главе. Причем, почему возникает шестигранная форма колонн понятно на примере ячеек Бенара, т.е. за счет образования стоячих волн. А вот сами колонны в магме могли образоваться только в тех местах нашей планеты, где время течет «вниз». В книге «Происхождение планеты Земля» рассказывалось, что в некоторых местах на Земле интенсивность выходящих волн времени очень высока. Они идут от земли вверх, наполняя все вокруг жизнью, способностью к самоорганизации. Такая энергия, втекая в системы, приводит их в более упорядоченное состояние, способствуя их эволюции. В других местах время наоборот устремляется к центру Земли, «вниз». Такой поток энергии является разрушительным, потому что это уже диссипативная энергия. Накладываясь на нашу систему стоячих волн, образованных в расплавленной магме, такой поток энергии разрушает молекулярные связи.

И как видно из рисунка, время втекает в каждую ячейку в центре вместе с динамическим потоком энергии. А вот вытекает время по краям ячейки. Вытекающее время уносит упорядоченность, другими словами, разрушает структуру. К тому же в этих местах дополнительно действуют диссипативные потоки, направленные к центру планеты. Поэтому по краям ячейки между молекулами базальта появляются разрушенные связи, следовательно, в этих местах сколы и системы трещин появляются проще всего. Такие характерные трещины возникают на всей протяженности остывающей магмы, образуя колонны длиной в десятки метров.

5. Заключение

Подведем итоги всему вышесказанному. Итак, мы рассмотрели, каким образом из неорганизованной и хаотичной материи возникают вдруг структуры, обладающие упорядоченностью и правильной геометрической формой, или как из хаоса возникает порядок. Вопрос этот далеко не праздный. Основная трагедия его предыстории в том, что когда Клазиус и Томсон (Кельвин) в 1865 году открыли закон, имеющий название второго начала термодинамики, то получили из него неожиданные выводы. Поскольку процессы рассеяния тепла (диссипация) необратимы, то рано или поздно все звезды погаснут, все активные процессы в природе прекратятся, и наступит состояние, которое Клаузиус назвал «тепловой смертью» Вселенной. Это все является следствием того, что самопроизвольные процессы идут только в сторону увеличении хаоса и беспорядка (энтропии). Горячее тело само по себе остыть может, но самопроизвольно нагреться не может никогда, прыгающий мяч всегда остановится, но покоящийся мяч самопроизвольно подпрыгивать не начнет.

Такая бессмысленность существования, навеянная тепловой смертью Вселенной, заставляла ученых кончать жизнь самоубийством. Покончил с собой Больцман, повесившись на оконном шнуре, в гостиничном номере в итальянском городе Дуино. Повесился младший сын Циолковского, работавший учителем в глухой степной деревне. По словам Зныкина, Козырев считал, что на них обоих повлияла безысходность, исходящая от тепловой смерти Вселенной.

Однако вопреки такому пессимистичному прогнозу, вызванному вторым началом термодинамики, мы видим, что Вселенная развивается и эволюционирует. Ни в одном уголке нашей Метагалактики мы не наблюдаем повсеместных процессов деградации. Это означает, что наряду с процессами, которые самопроизвольно происходят с повышением энтропии, должны быть такие самопроизвольные процессы, которые, наоборот увеличивают упорядоченность систем, или которые преобразуют простые вещества в сложные.

Впервые на явления такого рода обратил внимание И.Пригожин, получивший впоследствии за свои работы нобелевскую премию. На разнообразных физических и химических процессах он изучал способность систем к самоорганизации. В таких процессах молекулы, двигающиеся хаотично, вдруг начинали вести себя организованно и согласованно. При этом возникала упорядоченность, потому что в системе появлялись колебательные процессы. Яркими примерами таких самоорганизующихся процессов являются ячейки Бенара и химические часы, возникающие в реакции Белоусова – Жаботинского.

Самоорганизация, по определению Хакена, это спонтанное образование высокоупорядоченных структур из зародышей или даже хаоса, спонтанный переход от неупорядоченного состояния к упорядоченному за счет совместного, кооперативного (синхронного) действия многих подсистем. Из объяснений Пригожина мы видим, что под самоорганизацией он понимает преобразование хаотического движения молекул в автоколебательные. Из чего можно сделать вывод, что все колебательные процессы являются в какой-то мере самоорганизующими. Поэтому возникновение автоколебательных процессов из неколебательных движений, по мнению Пригожина, есть признак самоорганизации.

Однако в данной работе мы показали, что это не так. Потому что, следуя причинно-следственной логике, колебательные процессы не возникают сами по себе, они появляются на основе других колебательных процессов. Можно сказать, что одни колебания порождают другие колебания, что и является основным принципом причинно-следственных связей. Хотя, если мы не видим очевидных волновых процессов на начальном этапе, то это совсем не означает, что их нет. Так в процессе образования ячеек Бенара и в химической реакции Белоусова - Жаботинского волновые процессы на начальной стадии эксперимента отсутствуют в явном виде, но присутствуют в неявном. Зато на конечной стадии процесса волновые процессы присутствуют уже в явном виде. Они наблюдаются в виде стоячих волн на поверхности масла, и представлены появлением самих шестигранных ячеек. А в химической реакции Белоусова- Жаботинского колебательные процессы проявляются в чередовании химических реагентов.

Как было показано, колебательные процессы, которые превращали хаотическое движение в упорядоченное, были обусловлены волнами времени, которые втекали в систему «вместе» с поступающей энергией. Упорядоченное или колебательное движение в ячейках Бенара возникало в тот момент, когда градиент температуры, при котором скорость поступления тепла в систему становилась равной скорости волн времени, втекающих в систему. В этот момент наступает резонанс системы с внешним воздействием. А как мы знаем, при наступлении резонанса даже незначительное воздействие приводит к увеличению амплитуды колебаний, что в свою очередь приводит к возникновению волновых процессов, т.е. появляется упорядоченное движение. Таким образом, упорядоченное состояние в системе возникает, благодаря образованию стоячих волн в системе.

Следующий пример, в котором мы рассматривали, как из хаоса появляется порядок, относится к явлению, носящему названию фигуры Хладни. Здесь также основную роль в образовании порядка играют колебательные процессы. Песок, хаотично разбросанный по поверхности пластины при возникновении звуковых колебаний, начинал спонтанно перемещаться по поверхности, создавая правильные геометрические узоры. Этот пример интересен тем, что позволяет нам увидеть причудливую картину, которая возникает при образовании стоячих волн в пластине. Песок скапливается на линии узлов, четко вычерчивая области узлов и пучностей.

Именно на этом явлении, которое позволяет увидеть фигуры Хладни, можно объяснить правильную форму снежинок. Ведь, несмотря на всю кажущуюся простоту и привычность самой обыкновенной снежинки, наука до сих пор не может объяснить, как они образуются. Причем с точки зрения науки, мы хорошо знаем, где и при каких условиях появляются снежинки. Но вот почему на всех лучах снежинки повторяется один и тот же узор и откуда каждая молекула «знает» куда ей прикрепиться, чтобы соблюсти ту же геометрию, что и на других лучах, наука ответить не в состоянии. Но теперь, когда мы знаем, как ведет себя песок в фигурах Хладни и почему он так себя ведет, мы вполне можем обобщить этот вывод и для процессов образования снежинок. Ведь все молекулы водяного пара скапливаются вдоль узловых линий стоячих волн точно так же, как песок скапливается в узловых линиях на пластине, образуя фигуры Хладни.

Причем понять, как образуются стоячие волны в облаке, нам помогло явление ячеек Бенара. Когда на высоте примерно 10 км над землей между двумя тоненькими слоями воздуха появляется нужный температурный градиент, воздух приходит в конвективное движение, образуя ячейки подобно Бенаровским, где каждая такая ячейка представляет собой прообраз будущей снежинки. Потом в этих ячейках возникают стоячие волны. При этом движение молекул воздуха от конвективного переходит к колебательному, и молекулы пара постепенно смещаются к линиям узлов, так же как песок на пластине в экспериментах Хладни. Вдоль узловых линий молекулы пара уже не колеблются, поэтому могут смерзаться, образуя цельную ледяную конструкцию в виде снежинки.

Еще один пример образования порядка из хаоса относится также к очень интересному природному феномену, который называется «круги на полях». Как бы ни старались объяснить это явление проделками неких злоумышленников или шутников, но тот факт, что сложные пиктограммы, которые иногда возникают на полях, невозможно воссоздать даже при помощи современной техники, говорит о том, что их природа не является делом рук человеческих. Не являются они также и сообщениями инопланетян, которые, наверно, из благих побуждений пытаются оставить нам разные послания в такой форме. Трудно представить, что иных способов общаться с нами, у «бедных» инопланетян нет… Поэтому остается единственный логичный вывод, что их происхождение лежит в естественных природных процессах. Я, конечно же, имею в виду настоящие «круги», а не их подделки, коих сейчас насчитывается чуть ли не более 90 процентов от общего числа.

Появление кругов на полях обусловлено волнами времени, которые в определенные моменты могут создать сложные интерференционные картины в результате сложения волн от разных источников. Как и в любой интерференционной картине здесь есть линии ослабления амплитуд (линии узлов) и области усиления амплитуд (пучности). Если амплитуды волн складываются, то их влияние на биологические объекты усиливаются, и мы наблюдаем воздействие на растения на молекулярном уровне, под действием которого коленце растений изгибается. Хотя само растение продолжает расти дальше. В других местах, где происходит вычитание амплитуд, растения остаются не тронутыми. В результате на полях пшеницы образуется красивая геометрически правильная картина. В принципе этот процесс аналогичен тому, что мы рассматривали в образовании фигур Хладни. Только в отличие от фигур Хладни, которые создаются звуковыми волнами, круги на полях «рисуются» волнами времени.

В завершение рассматриваемой картины образования порядка из хаоса мы остановились на еще одном природном феномене – образовании шестигранных колонн, которые встречаются в некоторых местах нашей планеты. Феномен интересен тем, что трудно предположить, что это естественное природное явление, а не дело человеческих рук, настолько масштабно и грандиозно правильно выглядят они со стороны. Не смотря на то, что таких мест на планете несколько, тем не менее, это очень редкий природный феномен. Мы рассмотрели только несколько из известных мест. Одно из таких мест находится в Ирландии и известно как Дорога гигантов, другое в Вайоминге – это Чертова башня или Башня Дьявола, еще есть Фингалова пещера (Шотландия), Ущелье Garni (Армения), Призмы Базальта (Мексика), "органные трубы" – образование на горе Cargill в Новой Зеландии.

Объяснение тому, что образуются колонны шестигранной формы также лежит в природе времени. Очевидно, что в зоне трещин, которые делят сплошной монолит базальта на отдельные колонны, связь между молекулами ослаблена. Такое деструктурирующее влияние времени проявляется в некоторых местах земли, где время течет «вниз». В книге «Происхождение планеты Земля» рассказывалось, что в некоторых местах на Земле интенсивность выходящих волн времени очень высока. Они идут от земли вверх, наполняя все вокруг жизнью, способностью к самоорганизации. Такая энергия, втекая в системы, приводит их в более упорядоченное состояние, способствуя их эволюции. В других местах время наоборот устремляется к центру Земли, «вниз». Такой поток энергии является разрушительным, потому что это уже диссипативная энергия. Накладываясь на нашу систему стоячих волн, образованных в расплавленной магме, такой поток энергии разрушает молекулярные связи.

В нашей системе, связанной с застывающей магмой, мы имеем дела с двумя потоками волн времени. Одни поток – это динамическая энергия, она связанна с самим процессом изливания магмы, т.е. она определяет ту силу, что выталкивает магму на поверхность земли. Эти волны времени создают в магме ячейки подобные бенаровским. Другой поток волн времени, определяющий диссипативную энергию, разрушает молекулярные связи. Наибольшее влияние они оказывают в тех местах, где их направления совпадают. Как было показано на рисунке такими местами и являются границы ячеек Бенара. Поэтому и возникают грандиозные структуры в виде шестигранных колонн.

Таким образом, мы определили, что существует диссипативная энергия, которая обладает деструктурирующими свойствами, т.е. такими, которые разрушают систему. Именно диссипативная энергия отвечает за то, что в природе возрастает беспорядок и хаос, а значит, и энтропия. Благодаря этой энергии, один из основных законов термодинамики утверждает, что рано или поздно все звезды погаснут, все активные процессы в природе прекратятся, и наступит «тепловая смерть» Вселенной.

Однако помимо диссипативной энергии существует еще и динамическая энергия, которую время переносит от системы к системе, по утверждению Козырева. Во всех рассматриваемых нами примерах самоорганизации время играет структурообразующую роль. Порядок из хаоса возникает благодаря волнам времени, которые втекают в систему в виде динамической энергии. Неся в себе колебательную природу движений, волны времени оказывают влияние на материю на молекулярном уровне. В некоторых случаях хаотичное движение молекул в условиях резонанса становится циркулирующим и упорядоченным в пространстве, в других – периодичным во времени, в-третьих – возникают неподвижные картины интерференции, как при воздействии на биологические системы. И именно эту энергию мы называем динамической энергией, потому что она обладает структурообразующими свойствами. Можно сказать, что в основе образования нашей Вселенной лежит важнейший принцип самоорганизации материи, который обусловлен организующими свойствами времени. Этот принцип проявляется на всех уровнях мироздания.

[1] Иммане́нтность (лат. immanens, род.пад. immanentis «пребывающий внутри») – философская категория, обозначающая неотъемлемость, внутреннюю связь в противоположность внешней.

Самоорганизация вещества в природе

Оглавление